[OpenVINS] Code Review

ros_subscribe_msckf.cpp

• main() [Done] 
  • callback_inertial() [Done]
  • sys->feed_measurement_imu() [Done]
    • propagator->feed_imu() [Done]
    • initializer->feed_imu() [Done]
• callback_monocular()
  • sys->feed_measurement_monocular() [Done]
    • trackFEATS->feed_monocular() [Done]
      [ if "use_klt" parameter true, then it use "TrackKLT". else it use "TrackDescriptor".
      for our system, we use "TrackKLT". so we look for "TrackKLT". ]
      • perform_detection_monocular() [Done]
      • perform_matching() [Done]
        • undistort_point() [Done]
          • undistort_point_brown() [Done]
      • database->update_feature() [Done]
    • try_to_initialize() [Done]
      • initializer->initialize_with_imu() [Done]
      • [IMU] state->_imu->set_value() [Done]
        • [Type::PoseJPL] _pose->set_value() [Done]
          • [Type::JPLQuat] _q->set_value() [Done]
            • ov_core::quat_2_Rot() [Done]
          • [Type::Vec] _p->set_value() [Done]
        • [Type::Vec] _v->set_value() [Done]
        • [Type::Vec] _bg->set_value() [Done]
        • [Type::Vec] _ba->set_value() [Done}
      • [IMU] state->_imu->set_fej() [Done]
        • [Type::PoseJPL] _pose->set_fej() [Done]
          • [Type::JPLQuat] _q->set_fej() [Done]
            • ov_core::quat_2_Rot() [Done]
        • [Type::Vec] _v->set_fej() [Done]
        • [Type::Vec] _bg->set_fej() [Done]
        • [Type::Vec] _ba->set_fej() [Done]
      • cleanup_measurements() [Done]
        • clean_older_measurements() [Done}
    • do_feature_propagate_update()
      • [Propagator] propagator->propagate_and_clone() [Done]
        • select_imu_readings() [Done]
          • Propagator::interpolate_data() [Done]
        • predict_and_compute() [half done]
          • predict_mean_rk4() [Done]
            [ if "use_rk4_integration" parameter true, then it use "predict_mean_rk4". else it use "predict_mean_discrete()". for out system, we use "rk4_integration". so we look for "predict_mean_rk4()". ]
        • StateHelper::EKFPropagation() [half done]
        • StateHelper::augment_clone() [half done]
          • StateHelper::clone() [Done]
            • check_if_same_variable() [Done]
            • type_check->clone() [Done]
            • new_clone->set_local_id() [Done]
      • trackFEATS->get_feature_database()->features_not_containing_newer() [Done]
      • trackFEATS->get_feature_database()->features_containing() [Done]
      • trackFEATS->get_feature_database()->get_feature() [Done]
      • StateHelper::marginalize_slam() [Done]
        • StateHelper::marginalize() [Done]
      • [UdaterMSCKF]
        • clean_old_measurements() [Done]
        • initializer_feat->single_triangulation() [half done]
        • initializer_feat->single_gaussnewton() [halfdone]
          • FeatureInitializer::compute_error() [half done]
        • LandmarkRepresentation::is_relative_representation()
        • UpdateHelper::get_feature_jacobian_full()
        • UpdateHelper::get_feature_jacobian_representation()
        • UpdateHelper::get_feature_jacobian_intrinsics()
      • updaterSLAM->update()
      •  

updaterMSCKF->update()

 

 

 

 

 

 

main()

ros 설정 및 subscriber가 구동되게 된다.

IMU 센서와 관련된 callback_inertial 함수와 

Camera 센서와 관련된 callback_monocular 함수가 작동된다.

그 외에 알고리즘에 크게 관여하는 부분은 없으니, 넘어가도록 하자.

// Main function
int main(int argc, char** argv) {

    // Launch our ros node
    ros::init(argc, argv, "run_subscribe_msckf");
    ros::NodeHandle nh("~");

    // Create our VIO system
    VioManagerOptions params = parse_ros_nodehandler(nh);
    sys = new VioManager(params);
    viz = new RosVisualizer(nh, sys);


    //===================================================================================
    //===================================================================================
    //===================================================================================

    // Our camera topics (left and right stereo)
    std::string topic_imu;
    std::string topic_camera0, topic_camera1;
    nh.param<std::string>("topic_imu", topic_imu, "/imu0");
    nh.param<std::string>("topic_camera0", topic_camera0, "/cam0/image_raw");
    nh.param<std::string>("topic_camera1", topic_camera1, "/cam1/image_raw");

    // Logic for sync stereo subscriber
    // https://answers.ros.org/question/96346/subscribe-to-two-image_raws-with-one-function/?answer=96491#post-id-96491
    message_filters::Subscriber<sensor_msgs::Image> image_sub0(nh,topic_camera0.c_str(),1);
    message_filters::Subscriber<sensor_msgs::Image> image_sub1(nh,topic_camera1.c_str(),1);
    //message_filters::TimeSynchronizer<sensor_msgs::Image,sensor_msgs::Image> sync(image_sub0,image_sub1,5);
    typedef message_filters::sync_policies::ApproximateTime<sensor_msgs::Image, sensor_msgs::Image> sync_pol;
    message_filters::Synchronizer<sync_pol> sync(sync_pol(5), image_sub0,image_sub1);

    // Create subscribers
    ros::Subscriber subimu = nh.subscribe(topic_imu.c_str(), 9999, callback_inertial);
    ros::Subscriber subcam;
    if(params.state_options.num_cameras == 1) {
        ROS_INFO("subscribing to: %s", topic_camera0.c_str());
        subcam = nh.subscribe(topic_camera0.c_str(), 1, callback_monocular);
    } else if(params.state_options.num_cameras == 2) {
        ROS_INFO("subscribing to: %s", topic_camera0.c_str());
        ROS_INFO("subscribing to: %s", topic_camera1.c_str());
        sync.registerCallback(boost::bind(&callback_stereo, _1, _2));
    } else {
        ROS_ERROR("INVALID MAX CAMERAS SELECTED!!!");
        std::exit(EXIT_FAILURE);
    }

    //===================================================================================
    //===================================================================================
    //===================================================================================

    // Spin off to ROS
    ROS_INFO("done...spinning to ros");
    ros::spin();

    // Final visualization
    viz->visualize_final();

    // Finally delete our system
    delete sys;
    delete viz;


    // Done!
    return EXIT_SUCCESS;


}

 

 

 

callback_inertial() 

 

message가 수신된 시간과 함께 회전 가속도 값과 이동 가속도 값을 feed_measurement_imu 함수에 파라미터로 전달하는 역할을 한다. 

visualize 부분은 일단 넘긴다.

void callback_inertial(const sensor_msgs::Imu::ConstPtr& msg) {

    // convert into correct format
    double timem = msg->header.stamp.toSec();
    Eigen::Vector3d wm, am;
    wm << msg->angular_velocity.x, msg->angular_velocity.y, msg->angular_velocity.z;
    am << msg->linear_acceleration.x, msg->linear_acceleration.y, msg->linear_acceleration.z;

    // send it to our VIO system
    sys->feed_measurement_imu(timem, wm, am);
    viz->visualize_odometry(timem);

}

 

 

sys->feed_measurement_imu()

propagator에 전달받은 imu 값을 전달받은 시간과 함께 넘겨주게 된다.

아래는 initialize를 위해 값을 넘겨주는 과정이다.

void VioManager::feed_measurement_imu(double timestamp, Eigen::Vector3d wm, Eigen::Vector3d am) {

    // Push back to our propagator
    propagator->feed_imu(timestamp,wm,am);

    // Push back to our initializer
    if(!is_initialized_vio) {
        initializer->feed_imu(timestamp, wm, am);
    }

}

 

 

propagator->feed_imu()

IMUDATA 구조체를 갖는 imudata vector에 전달된 값들을 저장하게 된다. 

이 때, 20 seconds 전의 imudata 들은 빠른 연산과 메모리 관리를 위해 지워주게 된다.

여기서 더 적절한 메모리 관리 방법에 대해 연구할 가치가 있다. 

        /**
         * @brief Stores incoming inertial readings
         * @param timestamp Timestamp of imu reading
         * @param wm Gyro angular velocity reading
         * @param am Accelerometer linear acceleration reading
         */
        void feed_imu(double timestamp, Eigen::Vector3d wm, Eigen::Vector3d am) {

            // Create our imu data object
            IMUDATA data;
            data.timestamp = timestamp;
            data.wm = wm;
            data.am = am;

            // Append it to our vector
            imu_data.emplace_back(data);

            // Sort our imu data (handles any out of order measurements)
            //std::sort(imu_data.begin(), imu_data.end(), [](const IMUDATA i, const IMUDATA j) {
            //    return i.timestamp < j.timestamp;
            //});

            // Loop through and delete imu messages that are older then 20 seconds
            // TODO: we should probably have more elegant logic then this
            // TODO: but this prevents unbounded memory growth and slow prop with high freq imu
            auto it0 = imu_data.begin();
            while(it0 != imu_data.end()) {
                if(timestamp-(*it0).timestamp > 20) {
                    it0 = imu_data.erase(it0);
                } else {
                    it0++;
                }
            }

        }

 

 

initializer->feed_imu()

Initializer에는 propagator와는 다른 imudata가 존재하며, 여기에는 initialize를 위해 3개의 imudata만을 갖는다.

void InertialInitializer::feed_imu(double timestamp, Eigen::Matrix<double,3,1> wm, Eigen::Matrix<double,3,1> am) {

    // Create our imu data object
    IMUDATA data;
    data.timestamp = timestamp;
    data.wm = wm;
    data.am = am;

    // Append it to our vector
    imu_data.emplace_back(data);

    // Delete all measurements older than three of our initialization windows
    auto it0 = imu_data.begin();
    while(it0 != imu_data.end() && it0->timestamp < timestamp-3*_window_length) {
        it0 = imu_data.erase(it0);
    }

}

 

 

 

callback_monocular()

 

image message를 받아 초기작업을 하는 callback 함수이다.

이루어지는 작업은 다음과 같다.

1. image message의 신뢰성 검사 및 흑백이미지로의 변환(MONO8)

2. 만약 buffer가 채워져있지 않으면 buffer 채우기.

3. 받은 image message의 header 정보와 image 정보를 VIO system에 feed 하기.

4. visualization 하기.

5. 기본적으로 "이 전"에 받은 image message 정보를 feed하게 되고, 현재 받은 image message 정보는 "이 전" 정보를 feed 한 후에 buffer에 넣게 된다.

void callback_monocular(const sensor_msgs::ImageConstPtr& msg0) {


    // Get the image
    cv_bridge::CvImageConstPtr cv_ptr;
    try {
        cv_ptr = cv_bridge::toCvShare(msg0, sensor_msgs::image_encodings::MONO8);
    } catch (cv_bridge::Exception &e) {
        ROS_ERROR("cv_bridge exception: %s", e.what());
        return;
    }

    // Fill our buffer if we have not
    if(img0_buffer.rows == 0) {
        time_buffer = cv_ptr->header.stamp.toSec();
        img0_buffer = cv_ptr->image.clone();
        return;
    }

    // send it to our VIO system
    sys->feed_measurement_monocular(time_buffer, img0_buffer, 0);
    viz->visualize();

    // move buffer forward
    time_buffer = cv_ptr->header.stamp.toSec();
    img0_buffer = cv_ptr->image.clone();

}

 

 

sys->feed_measurement_monocular()

image 정보를 이용한 전체적인 작업이 진행된다. 

내용은 다음과 같다.

1. 프로세싱 타임 체크 (rT1 & rT2)

2. Downsample, 만약 Downsampling을 하고자 한다면 이 부분에서 진행되게 된다.

3. TrackKLT 혹은 TrackDescriptor 클래스에 image message 정보를 feed 해준다.

4. VIO initialization이 이루어지지 않았다면 VIO initialization을 진행하게 된다. 

5. propagate와 update를 진행한다.

void VioManager::feed_measurement_monocular(double timestamp, cv::Mat& img0, size_t cam_id) {

    // Start timing
    rT1 =  boost::posix_time::microsec_clock::local_time();

    // Downsample if we are downsampling
    if(params.downsample_cameras) {
        cv::Mat img0_temp;
        cv::pyrDown(img0,img0_temp,cv::Size(img0.cols/2.0,img0.rows/2.0));
        img0 = img0_temp.clone();
    }

    // Feed our trackers
    trackFEATS->feed_monocular(timestamp, img0, cam_id);

    // If aruoc is avalible, the also pass to it
    if(trackARUCO != nullptr) {
        trackARUCO->feed_monocular(timestamp, img0, cam_id);
    }
    rT2 =  boost::posix_time::microsec_clock::local_time();

    // If we do not have VIO initialization, then try to initialize
    // TODO: Or if we are trying to reset the system, then do that here!
    if(!is_initialized_vio) {
        is_initialized_vio = try_to_initialize();
        if(!is_initialized_vio) return;
    }

    // Call on our propagate and update function
    do_feature_propagate_update(timestamp);


}

 

 

trackFEATS->feed_monocular()

void TrackKLT::feed_monocular(double timestamp, cv::Mat &img, size_t cam_id) {

    // Start timing
    rT1 =  boost::posix_time::microsec_clock::local_time();

    // Lock this data feed for this camera
    std::unique_lock<std::mutex> lck(mtx_feeds.at(cam_id));

    // Histogram equalize
    cv::equalizeHist(img, img);

    // Extract the new image pyramid
    std::vector<cv::Mat> imgpyr;
    cv::buildOpticalFlowPyramid(img, imgpyr, win_size, pyr_levels);
    rT2 =  boost::posix_time::microsec_clock::local_time();

    // If we didn't have any successful tracks last time, just extract this time
    // This also handles, the tracking initalization on the first call to this extractor
    if(pts_last[cam_id].empty()) {
        // Detect new features
        perform_detection_monocular(imgpyr, pts_last[cam_id], ids_last[cam_id]);
        // Save the current image and pyramid
        img_last[cam_id] = img.clone();
        img_pyramid_last[cam_id] = imgpyr;
        return;
    }

    // First we should make that the last images have enough features so we can do KLT
    // This will "top-off" our number of tracks so always have a constant number
    perform_detection_monocular(img_pyramid_last[cam_id], pts_last[cam_id], ids_last[cam_id]);
    rT3 =  boost::posix_time::microsec_clock::local_time();

    //===================================================================================
    //===================================================================================

    // Debug
    //printf("current points = %d,%d\n",(int)pts_left_last.size(),(int)pts_right_last.size());

    // Our return success masks, and predicted new features
    std::vector<uchar> mask_ll;
    std::vector<cv::KeyPoint> pts_left_new = pts_last[cam_id];

    // Lets track temporally
    perform_matching(img_pyramid_last[cam_id],imgpyr,pts_last[cam_id],pts_left_new,cam_id,cam_id,mask_ll);
    rT4 =  boost::posix_time::microsec_clock::local_time();

    //===================================================================================
    //===================================================================================

    // If any of our mask is empty, that means we didn't have enough to do ransac, so just return
    if(mask_ll.empty()) {
        img_last[cam_id] = img.clone();
        img_pyramid_last[cam_id] = imgpyr;
        pts_last[cam_id].clear();
        ids_last[cam_id].clear();
        printf(RED "[KLT-EXTRACTOR]: Failed to get enough points to do RANSAC, resetting.....\n" RESET);
        return;
    }

    // Get our "good tracks"
    std::vector<cv::KeyPoint> good_left;
    std::vector<size_t> good_ids_left;

    // Loop through all left points
    for(size_t i=0; i<pts_left_new.size(); i++) {
        // Ensure we do not have any bad KLT tracks (i.e., points are negative)
        if(pts_left_new[i].pt.x < 0 || pts_left_new[i].pt.y < 0)
            continue;
        // If it is a good track, and also tracked from left to right
        if(mask_ll[i]) {
            good_left.push_back(pts_left_new[i]);
            good_ids_left.push_back(ids_last[cam_id][i]);
        }
    }


    //===================================================================================
    //===================================================================================


    // Update our feature database, with theses new observations
    for(size_t i=0; i<good_left.size(); i++) {
        cv::Point2f npt_l = undistort_point(good_left.at(i).pt, cam_id);
        database->update_feature(good_ids_left.at(i), timestamp, cam_id,
                                 good_left.at(i).pt.x, good_left.at(i).pt.y,
                                 npt_l.x, npt_l.y);
    }

    // Move forward in time
    img_last[cam_id] = img.clone();
    img_pyramid_last[cam_id] = imgpyr;
    pts_last[cam_id] = good_left;
    ids_last[cam_id] = good_ids_left;
    rT5 =  boost::posix_time::microsec_clock::local_time();

    // Timing information
    //printf("[TIME-KLT]: %.4f seconds for pyramid\n",(rT2-rT1).total_microseconds() * 1e-6);
    //printf("[TIME-KLT]: %.4f seconds for detection\n",(rT3-rT2).total_microseconds() * 1e-6);
    //printf("[TIME-KLT]: %.4f seconds for temporal klt\n",(rT4-rT3).total_microseconds() * 1e-6);
    //printf("[TIME-KLT]: %.4f seconds for feature DB update (%d features)\n",(rT5-rT4).total_microseconds() * 1e-6, (int)good_left.size());
    //printf("[TIME-KLT]: %.4f seconds for total\n",(rT5-rT1).total_microseconds() * 1e-6);


}

// Start timing

rT1 = boost::posix_time::microsec_clock::local_time();

프로세스 타임 측정

 

// Lock this data feed for this camera

std::unique_lock<std::mutex> lck(mtx_feeds.at(cam_id));

변수가 여기서만 값이 변경되도록 mutex를 이용해 lock 해줌. 

mutex란?

 

// Histogram equalize

cv::equalizeHist(img, img);

 

histogram equalization을 수행해줌.

histogram equalization이란?

 

// Extract the new image pyramid

std::vector<cv::Mat> imgpyr;

cv::buildOpticalFlowPyramid(img, imgpyr, win_size, pyr_levels);

rT2 = boost::posix_time::microsec_clock::local_time();

 

이미지로부터 새로운 이미지 피라미드를 생성함.

image pyramid란?

 

// If we didn't have any successful tracks last time, just extract this time

// This also handles, the tracking initalization on the first call to this extractor

if(pts_last[cam_id].empty()) {

// Detect new features

perform_detection_monocular(imgpyr, pts_last[cam_id], ids_last[cam_id]);

// Save the current image and pyramid

img_last[cam_id] = img.clone();

img_pyramid_last[cam_id] = imgpyr;

return;

}

만일 이 전 이미지 피라미드에서 특징점이 검출되지 않은 경우,

해당 부분에서 perform_detection_monocular() 함수를 사용하여 특징점 검출을 수행한 후,

현재 이미지와 이미지 피라미드를 이 전 이미지와 이미지 피라미드로 만들어준 후 return 함.

 

// First we should make that the last images have enough features so we can do KLT

// This will "top-off" our number of tracks so always have a constant number

perform_detection_monocular(img_pyramid_last[cam_id], pts_last[cam_id], ids_last[cam_id]);

혹시나 특징점이 파라미터에서 설정한 개수만큼 충분히 나오지 않았을 경우를 대비하여 다시 한번 perform_detection_monocular() 함수를 실행해줌.

 

rT3 = boost::posix_time::microsec_clock::local_time();

프로세스 시간 특정 종료

 

// Debug

//printf("current points = %d,%d\n",(int)pts_left_last.size(),(int)pts_right_last.size());

검출된 특징점 개수를 디버깅 한다. 

여기서는 사용하지 않는다. 

left와 right로 구분되어 있는 것을 봐서는 스테레오 카메라 용인 것 같다.

 

// Our return success masks, and predicted new features

std::vector<uchar> mask_ll;

std::vector<cv::KeyPoint> pts_left_new = pts_last[cam_id];

mask_ll 에서는 이후 perform_matching() 함수를 통해 tracking 된 결과에 대한 정보가 담기게 되며,

pts_left_new 에는 perform_matching() 함수를 통해 이 전의 특징점들로부터 tracking된 새로운 이미지 피라미드의 특징점들이 담기게 된다.

 

// Lets track temporally

perform_matching(img_pyramid_last[cam_id],imgpyr,pts_last[cam_id],pts_left_new,cam_id,cam_id,mask_ll);

perform_matching 함수는 이 전의 이미지 피라미드와 이 전의 피라미드 값과 새로운 이미지 피라미드를 이용하여 tracking된 새로운 특징점을 pts_left_new 에 담게된다. 그리고 ransac 알고리즘을 통해 매칭된 결과를 mask_ll에 담는다.

 

rT4 = boost::posix_time::microsec_clock::local_time();

프로세스 종료 시간 측정

 

// If any of our mask is empty, that means we didn't have enough to do ransac, so just return

if(mask_ll.empty()) {

img_last[cam_id] = img.clone();

img_pyramid_last[cam_id] = imgpyr;

pts_last[cam_id].clear();

ids_last[cam_id].clear();

printf(RED "[KLT-EXTRACTOR]: Failed to get enough points to do RANSAC, resetting.....\n" RESET);

return;

}

만약 ransac 알고리즘을 통하여 얻은 매칭된 특징점이 존재하지 않는다면, 

현재 이미지와 이미지 피라미드를 이 전 이미지, 이미지 피라미드로 만들어주고,

이 전 특징점 정보와 id 정보를 clear 하게 된다.

그리고 return 해준다.

 

// Get our "good tracks"

std::vector<cv::KeyPoint> good_left;

std::vector<size_t> good_ids_left;

tracking 까지 진행된 후 얻어진 양호한 결과들을 담을 벡터를 만든다.

 

// Loop through all left points

for(size_t i=0; i<pts_left_new.size(); i++) {

// Ensure we do not have any bad KLT tracks (i.e., points are negative)

if(pts_left_new[i].pt.x < 0 || pts_left_new[i].pt.y < 0)

continue;

// If it is a good track, and also tracked from left to right

if(mask_ll[i]) {

good_left.push_back(pts_left_new[i]);

good_ids_left.push_back(ids_last[cam_id][i]);

}

}

제대로 tracking 된 결과들을 good_left 벡터와 good_ids_left 벡터에 담는다.

 

 

 

 

 

 

 

perform_detection_monocular()

해당 함수의 목적은 이미지 피라미드를 이용해 파라미터에서 설정한 개수만큼 특징점을 구해주는 것이다.

그리고 검출된 특징점들을 파라미터인 pts0에 담아준다.

이 부분은 수식도 들어가는 복잡한 부분이기 때문에 line by line review를 해보자.

void TrackKLT::perform_detection_monocular(const std::vector<cv::Mat> &img0pyr, std::vector<cv::KeyPoint> &pts0, std::vector<size_t> &ids0) {

    // Create a 2D occupancy grid for this current image
    // Note that we scale this down, so that each grid point is equal to a set of pixels
    // This means that we will reject points that less then grid_px_size points away then existing features
    // TODO: figure out why I need to add the windowsize of the klt to handle features that are outside the image bound
    // TODO: I assume this is because klt of features at the corners is not really well defined, thus if it doesn't get a match it will be out-of-bounds
    Eigen::MatrixXi grid_2d = Eigen::MatrixXi::Zero((int)(img0pyr.at(0).rows/min_px_dist)+15, (int)(img0pyr.at(0).cols/min_px_dist)+15);
    auto it0 = pts0.begin();
    auto it2 = ids0.begin();
    while(it0 != pts0.end()) {
        // Get current left keypoint
        cv::KeyPoint kpt = *it0;
        // Check if this keypoint is near another point
        if(grid_2d((int)(kpt.pt.y/min_px_dist),(int)(kpt.pt.x/min_px_dist)) == 1) {
            it0 = pts0.erase(it0);
            it2 = ids0.erase(it2);
            continue;
        }
        // Else we are good, move forward to the next point
        grid_2d((int)(kpt.pt.y/min_px_dist),(int)(kpt.pt.x/min_px_dist)) = 1;
        it0++;
        it2++;
    }

    // First compute how many more features we need to extract from this image
    int num_featsneeded = num_features - (int)pts0.size();

    // If we don't need any features, just return
    if(num_featsneeded < 1)
        return;

    // Extract our features (use fast with griding)
    std::vector<cv::KeyPoint> pts0_ext;
    Grider_FAST::perform_griding(img0pyr.at(0), pts0_ext, num_featsneeded, grid_x, grid_y, threshold, true);

    // Now, reject features that are close a current feature
    std::vector<cv::KeyPoint> kpts0_new;
    std::vector<cv::Point2f> pts0_new;
    for(auto& kpt : pts0_ext) {
        // See if there is a point at this location
        if(grid_2d((int)(kpt.pt.y/min_px_dist),(int)(kpt.pt.x/min_px_dist)) == 1)
            continue;
        // Else lets add it!
        kpts0_new.push_back(kpt);
        pts0_new.push_back(kpt.pt);
        grid_2d((int)(kpt.pt.y/min_px_dist),(int)(kpt.pt.x/min_px_dist)) = 1;
    }

    // Loop through and record only ones that are valid
    for(size_t i=0; i<pts0_new.size(); i++) {
        // update the uv coordinates
        kpts0_new.at(i).pt = pts0_new.at(i);
        // append the new uv coordinate
        pts0.push_back(kpts0_new.at(i));
        // move id foward and append this new point
        size_t temp = ++currid;
        ids0.push_back(temp);
    }

}

Eigen::MatrixXi grid_2d = Eigen::MatrixXi::Zero((int)(img0pyr.at(0).rows/min_px_dist)+15, (int)(img0pyr.at(0).cols/min_px_dist)+15);

Eigen::MatrixXi 는 Matrix<int,Dynamic,Dynamic>의 typedef 이다. 

즉 요소의 type은 int이며, 파라미터로 주어지는 raws와 cols의 값만큼 Matrix가 만들어지는 것이다.

또한 Eigen::MatrixXi::Zero 이기 때문에 모두 0값으로 채워질 것이다.

auto it0 = pts0.begin();

auto it2 = ids0.begin();

pts0와 ids0의 원 형태는 다음과 같다.

std::vector<cv::KeyPoint> pts0;

std::vector<cv::KeyPoint> ids0;

 

vector의 begin()은 vector의 beginning iterator를 반환한다.

 

while(it0 != pts0.end()) {

// Get current left keypoint

cv::KeyPoint kpt = *it0;

// Check if this keypoint is near another point

if(grid_2d((int)(kpt.pt.y/min_px_dist),(int)(kpt.pt.x/min_px_dist)) == 1) {

it0 = pts0.erase(it0);

it2 = ids0.erase(it2);

continue;

}

// Else we are good, move forward to the next point

grid_2d((int)(kpt.pt.y/min_px_dist),(int)(kpt.pt.x/min_px_dist)) = 1;

it0++;

it2++;

}

반복문이 돌면서 it0와 it2는 1씩 증가하게 될 것이다.

그리고 pts0 vector의 마지막 요소와 it0의 포인터가 같아진다면 반복문은 종료되게 된다.

 

keypoints의 points는 계속 변화하지만, min_px_dist로 나누는 범위 안에서 이미 1이 된 값이 존재한다면 그 이후에 feature points는 같은 그리드 안에서 중복될 경우 그냥 없애주게 된다.

 

그러므로 이 과정은 Current image의 2D occupancy grid에서 keypoints 부분들을 점유시켜주는 것이라 볼 수 있다.

 

// First compute how many more features we need to extract from this image

int num_featsneeded = num_features - (int)pts0.size();

초기에 parameter 설정으로 우리가 필요로 하는 feature의 개수를 정했다. 

해당 개수에서 현재 feature의 개수를 뺌으로써 우리가 필요로 하는 feature의 개수를 정하게 된다.

 

// If we don't need any features, just return

if(num_featsneeded < 1)

return;

만약 필요한 feature의 개수가 충족된다면 그냥 return한다.

 

// Extract our features (use fast with griding)

std::vector<cv::KeyPoint> pts0_ext;

Grider_FAST::perform_griding(img0pyr.at(0), pts0_ext, num_featsneeded, grid_x, grid_y, threshold, true);

여기서는 부족한 keypoints를 검출하기 위한 작업이 진행되는데,

특히 ov_core::Grider_FAST 클래스를 사용한다는 점이 중요하다.

Grider_FAST::perform_griding 은 grid 형태에 대해서 FAST 알고리즘을 수행하는 것이라고 보면 된다.

 

// Now, reject features that are close a current feature

std::vector<cv::KeyPoint> kpts0_new;

std::vector<cv::Point2f> pts0_new;

for(auto& kpt : pts0_ext) {

// See if there is a point at this location

if(grid_2d((int)(kpt.pt.y/min_px_dist),(int)(kpt.pt.x/min_px_dist)) == 1)

continue;

// Else lets add it!

kpts0_new.push_back(kpt);

pts0_new.push_back(kpt.pt);

grid_2d((int)(kpt.pt.y/min_px_dist),(int)(kpt.pt.x/min_px_dist)) = 1;

}

이제 새로 얻어진 feature points 들에 대해 같은 그리드 안에서 중복되는 keypoints는 제거해준다.

 

// Loop through and record only ones that are valid

for(size_t i=0; i<pts0_new.size(); i++) {

// update the uv coordinates

kpts0_new.at(i).pt = pts0_new.at(i);

// append the new uv coordinate

pts0.push_back(kpts0_new.at(i));

// move id foward and append this new point

size_t temp = ++currid;

ids0.push_back(temp);

}

이제 새로 구한 keypoints 들을 기존에 구했던 keypoints들에 append 해준다.

 

perform_matching()

ov_core::TrackKLT class | OpenVINS

perform_matching에서는 이전 image pyramid인 img0pyr와 이 전의 특징점인 kpts0, 그리고 현재 image pyramid인 img1pyr을 이용해서 tracking(optical flow)을 수행한다. 이 때, 인자로 받는 kpts0와 kpts1은 같다. mask_out는 track 된 특징점이 존재하는 픽셀이 1이 된다. 

void TrackKLT::perform_matching(const std::vector<cv::Mat>& img0pyr, const std::vector<cv::Mat>& img1pyr,
                                std::vector<cv::KeyPoint>& kpts0, std::vector<cv::KeyPoint>& kpts1,
                                size_t id0, size_t id1,
                                std::vector<uchar>& mask_out) {

    // We must have equal vectors
    assert(kpts0.size() == kpts1.size());

    // Return if we don't have any points
    if(kpts0.empty() || kpts1.empty())
        return;

    // Convert keypoints into points (stupid opencv stuff)
    std::vector<cv::Point2f> pts0, pts1;
    for(size_t i=0; i<kpts0.size(); i++) {
        pts0.push_back(kpts0.at(i).pt);
        pts1.push_back(kpts1.at(i).pt);
    }

    // If we don't have enough points for ransac just return empty
    // We set the mask to be all zeros since all points failed RANSAC
    if(pts0.size() < 10) {
        for(size_t i=0; i<pts0.size(); i++)
            mask_out.push_back((uchar)0);
        return;
    }

    // Now do KLT tracking to get the valid new points
    std::vector<uchar> mask_klt;
    std::vector<float> error;
    cv::TermCriteria term_crit = cv::TermCriteria(cv::TermCriteria::COUNT + cv::TermCriteria::EPS, 15, 0.01);
    cv::calcOpticalFlowPyrLK(img0pyr, img1pyr, pts0, pts1, mask_klt, error, win_size, pyr_levels, term_crit, cv::OPTFLOW_USE_INITIAL_FLOW);


    // Normalize these points, so we can then do ransac
    // We don't want to do ransac on distorted image uvs since the mapping is nonlinear
    std::vector<cv::Point2f> pts0_n, pts1_n;
    for(size_t i=0; i<pts0.size(); i++) {
        pts0_n.push_back(undistort_point(pts0.at(i),id0));
        pts1_n.push_back(undistort_point(pts1.at(i),id1));
    }

    // Do RANSAC outlier rejection (note since we normalized the max pixel error is now in the normalized cords)
    std::vector<uchar> mask_rsc;
    double max_focallength_img0 = std::max(camera_k_OPENCV.at(id0)(0,0),camera_k_OPENCV.at(id0)(1,1));
    double max_focallength_img1 = std::max(camera_k_OPENCV.at(id1)(0,0),camera_k_OPENCV.at(id1)(1,1));
    double max_focallength = std::max(max_focallength_img0,max_focallength_img1);
    cv::findFundamentalMat(pts0_n, pts1_n, cv::FM_RANSAC, 1/max_focallength, 0.999, mask_rsc);

    // Loop through and record only ones that are valid
    for(size_t i=0; i<mask_klt.size(); i++) {
        auto mask = (uchar)((i < mask_klt.size() && mask_klt[i] && i < mask_rsc.size() && mask_rsc[i])? 1 : 0);
        mask_out.push_back(mask);
    }

    // Copy back the updated positions
    for(size_t i=0; i<pts0.size(); i++) {
        kpts0.at(i).pt = pts0.at(i);
        kpts1.at(i).pt = pts1.at(i);
    }

}

// We must have equal vectors

assert(kpts0.size() == kpts1.size());

먼저 kpts0와 kpts1이 갖고 있는 특징점 개수가 같은지 확인한다.

함수가 실행되기전 kpts1은 kpts0를 복사한 값이므로 같아야 정상이다.

assert는 예외상황에 대한 에러를 출력하는 함수이다.

 

// Return if we don't have any points

if(kpts0.empty() || kpts1.empty())

return;

특징점이 하나라도 검출되지 않는다면 반환한다.

 

// Convert keypoints into points (stupid opencv stuff)

std::vector<cv::Point2f> pts0, pts1;

for(size_t i=0; i<kpts0.size(); i++) {

pts0.push_back(kpts0.at(i).pt);

pts1.push_back(kpts1.at(i).pt);

}

차후에 cv::calcOpticalFlowPyrLK() 함수에 적용하기 위해서는 cv::Keypoints를 cv::Point2f 형태로 바꾸어야 한다.

cv::Keypoints를 굳이 cv::Point2f로 변환해서 사용해야 하기 때문에 저자는 "stupid opencv stuff" 이라고 이야기하고 있다...ㅋㅋㅋ;;

 

// If we don't have enough points for ransac just return empty

// We set the mask to be all zeros since all points failed RANSAC

if(pts0.size() < 10) {

for(size_t i=0; i<pts0.size(); i++)

mask_out.push_back((uchar)0);

return;

}

차후에 ransac 알고리즘도 수행하게 될텐데, 이 때, 충분한 특징점이 존재하지 않는다면 ransac 알고리즘을 수행할 수 없으므로 return을 하게 된다.

ransac에 실패하기 때문에 mask_out은 모두 0으로 설정하게 되는데 "굳이 해야하나?" 라는 의문도 있다.  

 

// Now do KLT tracking to get the valid new points

std::vector<uchar> mask_klt;

std::vector<float> error;

cv::TermCriteria term_crit = cv::TermCriteria(cv::TermCriteria::COUNT + cv::TermCriteria::EPS, 15, 0.01);

cv::calcOpticalFlowPyrLK(img0pyr, img1pyr, pts0, pts1, mask_klt, error, win_size, pyr_levels, term_crit, cv::OPTFLOW_USE_INITIAL_FLOW);

이제 cv::calcOpticalFlowPyrLK() 함수를 사용하여 KLT tracking을 수행한다. 

이 때, 입력으로 단일 이미지를 줄 수도 있지만, image pyramid 를 줄 수도 있다.

여기서는 image pyramid를 주게 되며, 

pts0는 입력으로 flow 판단의 기준좌표가 되고, pts1은 출력으로써 계산된 새로운 특징점의 위치를 갖는다.

mask_klt : mask_klt는 tracking이 된 경우 1이 set되고, 그렇지 않은 경우 0으로 set된다.

error : error의 경우 모든 tracking된 특징점은 error를 갖게 되는데, 이 error의 값은 flag(ex. OPTFLOW_USE_INITIAL_FLOW)에 따라서 정해진다. 

winSize : 알고리즘에서 각각의 pyramid level에 대한 search window의 크기를 의미한다.

pyr_levels : pyramid level을 어느 정도로 설정할지이다. 0인 경우 pyramid를 사용하지 않게 되고, 1인 경우 2개 level의 pyramid를 사용하게 되는 식으로 확장된다.

criteria : iterative search algorithm 을 언제 종료(Termination)할지에 대한 기준(Criteria)을 만들게 된다. 반복횟수인 Count는 15회가 넘어갈 때, search window가 Epsilon이 0.01 미만으로 이동할 때가 종료 기준이 된다.

 

// Normalize these points, so we can then do ransac

// We don't want to do ransac on distorted image uvs since the mapping is nonlinear

std::vector<cv::Point2f> pts0_n, pts1_n;

for(size_t i=0; i<pts0.size(); i++) {

pts0_n.push_back(undistort_point(pts0.at(i),id0));

pts1_n.push_back(undistort_point(pts1.at(i),id1));

}

ransac을 진행하기 전에 검출되고 tracking된 특징점들에 대해 왜곡보정을 수행한다.

자세한 왜곡보정 방법은 해당 함수에 대한 리뷰를 확인하자.

 

// Do RANSAC outlier rejection (note since we normalized the max pixel error is now in the normalized cords)

std::vector<uchar> mask_rsc;

double max_focallength_img0 = std::max(camera_k_OPENCV.at(id0)(0,0),camera_k_OPENCV.at(id0)(1,1));

double max_focallength_img1 = std::max(camera_k_OPENCV.at(id1)(0,0),camera_k_OPENCV.at(id1)(1,1));

double max_focallength = std::max(max_focallength_img0,max_focallength_img1);

cv::findFundamentalMat(pts0_n, pts1_n, cv::FM_RANSAC, 1/max_focallength, 0.999, mask_rsc);

camera_k_OPENCV 는 다음과 같은 형을 갖는다.

std::map<size_t, cv::Matx33d> camera_k_OPENCV;

map container는 key와 value가 쌍으로 저장되는 형태이며, 

여기서는 cam의 id와 해당 카메라의 cameraMatrix가 쌍으로 저장되게 된다.

 

cameraMatrix는 다음과 같은 형태를 갖는다.

camera matrix

보다시피 (0,0) 과 (1,1) 이 focallength 가 되는데, 이 focallength 중 가장 큰 값을 선정하게 되는 것이다.

 

그리고 드디어 fundamental matrix를 구하게 된다.

Fundamental Matrix에 대한 자세한 설명은 이 블로그를 참고하면 좋겠다. 

 

간단히 이야기 하면 A, B 두 영상이 존재할 때, A영상에 존재하는 특징점을 B영상의 에피폴라 라인에 사영시키기 위하여 필요한 행렬이 Fundamental Matrix라고 볼 수 있다.

 

cv::findFundamentalMat() 함수는 두 영상에 존재하는 각각의 특징점을 입력으로 하여 RANSAC 알고리즘을 사용하여 fundamental matrix를 찾아서 반환해주게 되는데, 여기에서는 fundamental matrix를 반환받지는 않고, outlier를 제거하고 inlier만 구하기 위한 방법으로 사용했다.

 

pts0_n : 첫 번째 이미지 프레임의 특징점

pts1_n : 두 번째 이미지 프레임의 특징점

cv::FM_RANSAC : 사용할 알고리즘 (RANSAC)

1/max_focallength : RANSAC 알고리즘을 위해 사용되는 파라미터. point와 epipolar line의 최대 거리라고 하는데, 보통 1에서 3의 값을 준다고 한다. 그런데 여기에서는 왜 1을 max_focallength로 나누었는지 모르겠다.

### 해당 의문에 대한 github issue ###

 0.999 : 해당 파라미터는 확신을 위한 이상적인 레벨에 대한 내용이다. 즉, inlier에 대한 확률과 관련한 파라미터라고 보면 된다.

mask_rsc : 해당 마스크는 uchar 형의 vector이며, outliers로 판단되는 특징점은 0으로, inlier로 판단되는 특징점은 1로 set 된다.

 

// Loop through and record only ones that are valid

for(size_t i=0; i<mask_klt.size(); i++) {

auto mask = (uchar)((i < mask_klt.size() && mask_klt[i] && i < mask_rsc.size() && mask_rsc[i])? 1 : 0);

mask_out.push_back(mask);

}

이제 특징점들 중 outlier가 아닌 것들만 mask_out vector에 저장해준다.

 

// Copy back the updated positions

for(size_t i=0; i<pts0.size(); i++) {

kpts0.at(i).pt = pts0.at(i);

kpts1.at(i).pt = pts1.at(i);

}

이제 특징점들을 초반에 받은 파라미터 벡터에 담아준다.

 

undistort_point()

해당 함수에서는 카메라의 cameraMatrix와 distCoeffs를 불러와 왜곡보정을 위한 함수를 실행해주는데,

우리는 단안카메라를 사용하니, undistort_point_brown() 함수가 사용될 것이다.

여기까지만 알면 되겠다.

        /**
         * @brief Main function that will undistort/normalize a point.
         * @param pt_in uv 2x1 point that we will undistort
         * @param cam_id id of which camera this point is in
         * @return undistorted 2x1 point
         *
         * Given a uv point, this will undistort it based on the camera matrices.
         * This will call on the model needed, depending on what type of camera it is!
         * So if we have fisheye for camera_1 is true, we will undistort with the fisheye model.
         * In Kalibr's terms, the non-fisheye is `pinhole-radtan` while the fisheye is the `pinhole-equi` model.
         */
        cv::Point2f undistort_point(cv::Point2f pt_in, size_t cam_id) {
            // Determine what camera parameters we should use
            cv::Matx33d camK = this->camera_k_OPENCV.at(cam_id);
            cv::Vec4d camD = this->camera_d_OPENCV.at(cam_id);
            // Call on the fisheye if we should!
            if (this->camera_fisheye.at(cam_id)) {
                return undistort_point_fisheye(pt_in, camK, camD);
            }
            return undistort_point_brown(pt_in, camK, camD);
        }

 

undistort_point_brown()

해당 함수는 단안카메라에서 이미지의 특징점 포인트에 대해 왜곡을 보정하는 함수이다. 

        /**
         * @brief Undistort function RADTAN/BROWN.
         *
         * Given a uv point, this will undistort it based on the camera matrices.
         * To equate this to Kalibr's models, this is what you would use for `pinhole-radtan`.
         */
        cv::Point2f undistort_point_brown(cv::Point2f pt_in, cv::Matx33d &camK, cv::Vec4d &camD) {
            // Convert to opencv format
            cv::Mat mat(1, 2, CV_32F);
            mat.at<float>(0, 0) = pt_in.x;
            mat.at<float>(0, 1) = pt_in.y;
            mat = mat.reshape(2); // Nx1, 2-channel
            // Undistort it!
            cv::undistortPoints(mat, mat, camK, camD);
            // Construct our return vector
            cv::Point2f pt_out;
            mat = mat.reshape(1); // Nx2, 1-channel
            pt_out.x = mat.at<float>(0, 0);
            pt_out.y = mat.at<float>(0, 1);
            return pt_out;
        }

// Convert to opencv format

cv::Mat mat(1, 2, CV_32F);

mat.at<float>(0, 0) = pt_in.x;

mat.at<float>(0, 1) = pt_in.y;

mat = mat.reshape(2); // Nx1, 2-channel

먼저 포인트를 1행 2열의 매트릭스에 담게된다.

그리고 reshape 함수를 사용하게 되는데,

cv::Mat::reshape 함수는 Matrix의 형태를 변경해준다고 보면 된다.

Mat cv::Mat::reshape( int cn, int rows=0 ) const 형태를 지니며,

cn은 변경될 채널의 수, rows는 변경될 행의 수이다.

두 값 모두 0으로 설정할 시 기존의 채널과 rows를 유지한다.

즉 여기에서는 1행 2열의 Matrix를 rows(1)를 유지하며 채널은 2채널로 변경하는 것이다.

여기서 채널이라고 하면, 다음과 같이 이해할 수 있다.

그레이 영상의 경우 채널은 1이고, 컬러영상의 경우 채널은 3이다.

한 픽셀당 갖는 값이 1인지 3인지에 대한 구분이다.

 

예를들어 3x3 크기의 이미지가 존재한다면 그레이영상과 컬러영상의 형태는 다음과 같게 된다.

 

그레이영상(1채널, 픽셀당 1개의 값)

255	255	255
255	255	255
255	255	255

컬러영상(3채널, 픽셀당 3개의 값)

255	255	255	255	255	255	255	255	255
255	255	255	255	255	255	255	255	255
255	255	255	255	255	255	255	255	255

 

즉, 1행 2열의 Matrix는 아래와 같고

value_1 (1행 1열)

value_2 (1행 2열)

mat.reshape(2) 후에는 다음과 같다.

value_1 (1행 1열)

value_2 (1행 1열)

 

// Undistort it!

cv::undistortPoints(mat, mat, camK, camD);

이후에 cv::undistortPoints 함수를 사용하여 왜곡을 보정하게 된다.

이 때, 입력 포인트가 담긴 Matrix가 mat이 되며, 왜곡보정된 출력 포인트 또한 mat이 된다.

파라미터로 camK와 camD를 주게 되는데,

camK는 cameraMatrix, camD는 distCoeffs가 된다.

camera Matrix는 주점, focal length 로 구성되며 다음과 같은 형태이다.

camera matrix

distCoeffs는 왜곡정보를 담은 것으로 다음과 같은 벡터 형태를 갖는다.

distCoeffs

// Construct our return vector

cv::Point2f pt_out;

mat = mat.reshape(1); // Nx2, 1-channel

pt_out.x = mat.at<float>(0, 0);

pt_out.y = mat.at<float>(0, 1);

return pt_out;

즉, mat을 reshape한 이유는 cv::undistortPoints 함수에 사용하기 위함이다.

그러므로 왜곡보정이 된 이후에는 다시 reshape하여 원래 형태(cv::Point2f)로 돌려주게 된다.

 

database->update_feature()

features_idlookup에 update 한다.

        /**
         * @brief Update a feature object
         * @param id ID of the feature we will update
         * @param timestamp time that this measurement occured at
         * @param cam_id which camera this measurement was from
         * @param u raw u coordinate
         * @param v raw v coordinate
         * @param u_n undistorted/normalized u coordinate
         * @param v_n undistorted/normalized v coordinate
         *
         * This will update a given feature based on the passed ID it has.
         * It will create a new feature, if it is an ID that we have not seen before.
         */
        void update_feature(size_t id, double timestamp, size_t cam_id,
                            float u, float v, float u_n, float v_n) {

            // Find this feature using the ID lookup
            std::unique_lock<std::mutex> lck(mtx);
            if (features_idlookup.find(id) != features_idlookup.end()) {
                // Get our feature
                Feature *feat = features_idlookup[id];
                // Append this new information to it!
                feat->uvs[cam_id].emplace_back(Eigen::Vector2f(u, v));
                feat->uvs_norm[cam_id].emplace_back(Eigen::Vector2f(u_n, v_n));
                feat->timestamps[cam_id].emplace_back(timestamp);
                return;
            }

            // Debug info
            //ROS_INFO("featdb - adding new feature %d",(int)id);

            // Else we have not found the feature, so lets make it be a new one!
            Feature *feat = new Feature();
            feat->featid = id;
            feat->uvs[cam_id].emplace_back(Eigen::Vector2f(u, v));
            feat->uvs_norm[cam_id].emplace_back(Eigen::Vector2f(u_n, v_n));
            feat->timestamps[cam_id].emplace_back(timestamp);

            // Append this new feature into our database
            features_idlookup.insert({id, feat});
        }

// Find this feature using the ID lookup

std::unique_lock<std::mutex> lck(mtx);

먼저 mutex를 사용해 lock 해준다.

 

if (features_idlookup.find(id) != features_idlookup.end()) {

// Get our feature

Feature *feat = features_idlookup[id];

// Append this new information to it!

feat->uvs[cam_id].emplace_back(Eigen::Vector2f(u, v));

feat->uvs_norm[cam_id].emplace_back(Eigen::Vector2f(u_n, v_n));

feat->timestamps[cam_id].emplace_back(timestamp);

return;

}

features_idlookup의 원형은 다음과 같다.

 

std::unordered_map<size_t, Feature *> features_idlookup;

 

unordered_map은 hash_map 구조를 갖는 데이터 형이며, 

key와 value 값을 갖는 데이터들을 빠르게 검색할 수 있다는 특징을 지닌다.

 

std::unordered_map::find 함수는 파라미터로 주어지는 key 값을 찾는 iterator이며,

해당 key 값을 찾았을 때는 해당 key 값과 매칭되는 value를 반환하게 되고, 찾지 못했을 경우는
std::unordered_map::end 를 반환하게 된다. 

 

즉, if (features_idlookup.find(id) != features_idlookup.end()) 는

key 값이 존재하는 경우에 작동하는 조건문이라고 보면 된다.

 

이 후에 

Feature *feat 이라는 포인터를 만들어서 features_idlookup[id] 의 주소를 가져와 Feature *feat에 건네주게 된다.

 

그리고 데이터들을 데이터베이스에 담는다.

 

// Else we have not found the feature, so lets make it be a new one!

Feature *feat = new Feature();

feat->featid = id;

feat->uvs[cam_id].emplace_back(Eigen::Vector2f(u, v));

feat->uvs_norm[cam_id].emplace_back(Eigen::Vector2f(u_n, v_n));

feat->timestamps[cam_id].emplace_back(timestamp);

// Append this new feature into our database

features_idlookup.insert({id, feat});

중복되는 id가 없는 feature는 새로운 features_idlookup 데이터베이스를 만들어 insert 해준다.

 

 

 

try_to_initialize()

bool VioManager::try_to_initialize() {

    // Returns from our initializer
    double time0;
    Eigen::Matrix<double, 4, 1> q_GtoI0;
    Eigen::Matrix<double, 3, 1> b_w0, v_I0inG, b_a0, p_I0inG;

    // Try to initialize the system
    bool success = initializer->initialize_with_imu(time0, q_GtoI0, b_w0, v_I0inG, b_a0, p_I0inG);

    // Return if it failed
    if (!success) {
        return false;
    }

    // Make big vector (q,p,v,bg,ba), and update our state
    // Note: start from zero position, as this is what our covariance is based off of
    Eigen::Matrix<double,16,1> imu_val;
    imu_val.block(0,0,4,1) = q_GtoI0;
    imu_val.block(4,0,3,1) << 0,0,0;
    imu_val.block(7,0,3,1) = v_I0inG;
    imu_val.block(10,0,3,1) = b_w0;
    imu_val.block(13,0,3,1) = b_a0;
    //imu_val.block(10,0,3,1) << 0,0,0;
    //imu_val.block(13,0,3,1) << 0,0,0;
    state->_imu->set_value(imu_val);
    state->_imu->set_fej(imu_val);
    state->_timestamp = time0;
    startup_time = time0;

    // Cleanup any features older then the initialization time
    trackFEATS->get_feature_database()->cleanup_measurements(state->_timestamp);
    if(trackARUCO != nullptr) {
        trackARUCO->get_feature_database()->cleanup_measurements(state->_timestamp);
    }

    // Else we are good to go, print out our stats
    printf(GREEN "[INIT]: orientation = %.4f, %.4f, %.4f, %.4f\n" RESET,state->_imu->quat()(0),state->_imu->quat()(1),state->_imu->quat()(2),state->_imu->quat()(3));
    printf(GREEN "[INIT]: bias gyro = %.4f, %.4f, %.4f\n" RESET,state->_imu->bias_g()(0),state->_imu->bias_g()(1),state->_imu->bias_g()(2));
    printf(GREEN "[INIT]: velocity = %.4f, %.4f, %.4f\n" RESET,state->_imu->vel()(0),state->_imu->vel()(1),state->_imu->vel()(2));
    printf(GREEN "[INIT]: bias accel = %.4f, %.4f, %.4f\n" RESET,state->_imu->bias_a()(0),state->_imu->bias_a()(1),state->_imu->bias_a()(2));
    printf(GREEN "[INIT]: position = %.4f, %.4f, %.4f\n" RESET,state->_imu->pos()(0),state->_imu->pos()(1),state->_imu->pos()(2));
    return true;

}

// Returns from our initializer

double time0;

Eigen::Matrix<double, 4, 1> q_GtoI0;

Eigen::Matrix<double, 3, 1> b_w0, v_I0inG, b_a0, p_I0inG;

선언

 

// Try to initialize the system

bool success = initializer->initialize_with_imu(time0, q_GtoI0, b_w0, v_I0inG, b_a0, p_I0inG);

initialize_with_imu() 함수를 통해 각 파라미터에 값이 들어감.

 

// Return if it failed

if (!success) {

return false;

}

intialization이 실패할 경우 return 함.

 

// Make big vector (q,p,v,bg,ba), and update our state

// Note: start from zero position, as this is what our covariance is based off of

Eigen::Matrix<double,16,1> imu_val;

imu_val.block(0,0,4,1) = q_GtoI0;

imu_val.block(4,0,3,1) << 0,0,0;

imu_val.block(7,0,3,1) = v_I0inG;

imu_val.block(10,0,3,1) = b_w0;

imu_val.block(13,0,3,1) = b_a0;

//imu_val.block(10,0,3,1) << 0,0,0;

//imu_val.block(13,0,3,1) << 0,0,0;

state->_imu->set_value(imu_val);

state->_imu->set_fej(imu_val);

state->_timestamp = time0;

startup_time = time0;

imu_val이라는 큰 Matrix를 만들어 값을 대입하게 된다.

 

Eigen::block은 다음과 같이 쓰인다.

matrix.block(i,j,p,q);

(p,q) 사이즈의 값들을 (i,j) 에 대입한다.

 

이 imu_val 을 state->_imu에도 set해준다. 

 

// Else we are good to go, print out our stats

printf(GREEN "[INIT]: orientation = %.4f, %.4f, %.4f, %.4f\n" RESET,state->_imu->quat()(0),state->_imu->quat()(1),state->_imu->quat()(2),state->_imu->quat()(3));

printf(GREEN "[INIT]: bias gyro = %.4f, %.4f, %.4f\n" RESET,state->_imu->bias_g()(0),state->_imu->bias_g()(1),state->_imu->bias_g()(2));

printf(GREEN "[INIT]: velocity = %.4f, %.4f, %.4f\n" RESET,state->_imu->vel()(0),state->_imu->vel()(1),state->_imu->vel()(2));

printf(GREEN "[INIT]: bias accel = %.4f, %.4f, %.4f\n" RESET,state->_imu->bias_a()(0),state->_imu->bias_a()(1),state->_imu->bias_a()(2));

printf(GREEN "[INIT]: position = %.4f, %.4f, %.4f\n" RESET,state->_imu->pos()(0),state->_imu->pos()(1),state->_imu->pos()(2));

return true;

디버깅

 

initialize_with_imu()

bool InertialInitializer::initialize_with_imu(double &time0, Eigen::Matrix<double,4,1> &q_GtoI0, Eigen::Matrix<double,3,1> &b_w0,
                                              Eigen::Matrix<double,3,1> &v_I0inG, Eigen::Matrix<double,3,1> &b_a0, Eigen::Matrix<double,3,1> &p_I0inG) {

    // Return if we don't have any measurements
    if(imu_data.empty()) {
        return false;
    }

    // Newest imu timestamp
    double newesttime = imu_data.at(imu_data.size()-1).timestamp;

    // First lets collect a window of IMU readings from the newest measurement to the oldest
    std::vector<IMUDATA> window_newest, window_secondnew;
    for(IMUDATA data : imu_data) {
        if(data.timestamp > newesttime-1*_window_length && data.timestamp <= newesttime-0*_window_length) {
            window_newest.push_back(data);
        }
        if(data.timestamp > newesttime-2*_window_length && data.timestamp <= newesttime-1*_window_length) {
            window_secondnew.push_back(data);
        }
    }

    // Return if both of these failed
    if(window_newest.empty() || window_secondnew.empty()) {
        //printf(YELLOW "InertialInitializer::initialize_with_imu(): unable to select window of IMU readings, not enough readings\n" RESET);
        return false;
    }

    // Calculate the sample variance for the newest one
    Eigen::Matrix<double,3,1> a_avg = Eigen::Matrix<double,3,1>::Zero();
    for(IMUDATA data : window_newest) {
        a_avg += data.am;
    }
    a_avg /= (int)window_newest.size();
    double a_var = 0;
    for(IMUDATA data : window_newest) {
        a_var += (data.am-a_avg).dot(data.am-a_avg);
    }
    a_var = std::sqrt(a_var/((int)window_newest.size()-1));

    // If it is below the threshold just return
    if(a_var < _imu_excite_threshold) {
        printf(YELLOW "InertialInitializer::initialize_with_imu(): no IMU excitation, below threshold %.4f < %.4f\n" RESET,a_var,_imu_excite_threshold);
        return false;
    }

    // Return if we don't have any measurements
    //if(imu_data.size() < 200) {
    //    return false;
    //}

    // Sum up our current accelerations and velocities
    Eigen::Vector3d linsum = Eigen::Vector3d::Zero();
    Eigen::Vector3d angsum = Eigen::Vector3d::Zero();
    for(size_t i=0; i<window_secondnew.size(); i++) {
        linsum += window_secondnew.at(i).am;
        angsum += window_secondnew.at(i).wm;
    }

    // Calculate the mean of the linear acceleration and angular velocity
    Eigen::Vector3d linavg = Eigen::Vector3d::Zero();
    Eigen::Vector3d angavg = Eigen::Vector3d::Zero();
    linavg = linsum/window_secondnew.size();
    angavg = angsum/window_secondnew.size();

    // Get z axis, which alines with -g (z_in_G=0,0,1)
    Eigen::Vector3d z_axis = linavg/linavg.norm();

    // Create an x_axis
    Eigen::Vector3d e_1(1,0,0);

    // Make x_axis perpendicular to z
    Eigen::Vector3d x_axis = e_1-z_axis*z_axis.transpose()*e_1;
    x_axis= x_axis/x_axis.norm();

    // Get z from the cross product of these two
    Eigen::Matrix<double,3,1> y_axis = skew_x(z_axis)*x_axis;

    // From these axes get rotation
    Eigen::Matrix<double,3,3> Ro;
    Ro.block(0,0,3,1) = x_axis;
    Ro.block(0,1,3,1) = y_axis;
    Ro.block(0,2,3,1) = z_axis;

    // Create our state variables
    Eigen::Matrix<double,4,1> q_GtoI = rot_2_quat(Ro);

    // Set our biases equal to our noise (subtract our gravity from accelerometer bias)
    Eigen::Matrix<double,3,1> bg = angavg;
    Eigen::Matrix<double,3,1> ba = linavg - quat_2_Rot(q_GtoI)*_gravity;


    // Set our state variables
    time0 = window_secondnew.at(window_secondnew.size()-1).timestamp;
    q_GtoI0 = q_GtoI;
    b_w0 = bg;
    v_I0inG = Eigen::Matrix<double,3,1>::Zero();
    b_a0 = ba;
    p_I0inG = Eigen::Matrix<double,3,1>::Zero();

    // Done!!!
    return true;


}

// Return if we don't have any measurements

if(imu_data.empty()) {

return false;

}

imu_data 체크

 

// Newest imu timestamp

double newesttime = imu_data.at(imu_data.size()-1).timestamp;

가장 최근 imu_data 의 time을 가져온다.

 

// First lets collect a window of IMU readings from the newest measurement to the oldest

std::vector<IMUDATA> window_newest, window_secondnew;

for(IMUDATA data : imu_data) {

if(data.timestamp > newesttime-1*_window_length && data.timestamp <= newesttime-0*_window_length) {

window_newest.push_back(data);

}

if(data.timestamp > newesttime-2*_window_length && data.timestamp <= newesttime-1*_window_length) {

window_secondnew.push_back(data);

}

}

해당 부분에서는 window_newest 와 window_secondnew에 imu data를 담아주게 되는데,

초기에 설정하게 되는 _window_length를 기준으로 더 최근 imu data를 window_newest에, 

더 과거의 imu data를 window_secondnew에 담아주게 된다.

 

// Return if both of these failed

if(window_newest.empty() || window_secondnew.empty()) {

//printf(YELLOW "InertialInitializer::initialize_with_imu(): unable to select window of IMU readings, not enough readings\n" RESET);

return false;

}

만약 window_newest 또는 window_secondnew에 아무 데이터도 존재하지 않는다면 return해준다.

 

// Calculate the sample variance for the newest one

Eigen::Matrix<double,3,1> a_avg = Eigen::Matrix<double,3,1>::Zero();

for(IMUDATA data : window_newest) {

a_avg += data.am;

}

a_avg /= (int)window_newest.size();

double a_var = 0;

for(IMUDATA data : window_newest) {

a_var += (data.am-a_avg).dot(data.am-a_avg);

}

a_var = std::sqrt(a_var/((int)window_newest.size()-1));

가장 최근 가속도에 대한 imu data들을 이용해서 평균을 내어 a_avg에 담아준다.

 

.dot 연산은 곱하기 연산이다.

그러므로 (data.am-a_avg) * (data.am-a_avg) 를 a_var에 더해준다고 보면 된다.

 

이후에 a_var을 window_newest로 나누어 평균을 구하고, 루트(sqrt)를 취해주어 분산(a_var)을 구하게 된다.

 

// If it is below the threshold just return

if(a_var < _imu_excite_threshold) {

printf(YELLOW "InertialInitializer::initialize_with_imu(): no IMU excitation, below threshold %.4f < %.4f\n" RESET,a_var,_imu_excite_threshold);

return false;

}

초기에 설정하는 imu threshold 보다 구해진 a_var 분산값이 낮다면 return한다. 

 

// Sum up our current accelerations and velocities

Eigen::Vector3d linsum = Eigen::Vector3d::Zero();

Eigen::Vector3d angsum = Eigen::Vector3d::Zero();

for(size_t i=0; i<window_secondnew.size(); i++) {

linsum += window_secondnew.at(i).am;

angsum += window_secondnew.at(i).wm;

}

이제 가장 최근의 imu data들의 vector인 window_secondnew에서

가속도값들의 합 linsum과 회전 가속도 값들의 합 angsum을 구해준다.

 

// Calculate the mean of the linear acceleration and angular velocity

Eigen::Vector3d linavg = Eigen::Vector3d::Zero();

Eigen::Vector3d angavg = Eigen::Vector3d::Zero();

linavg = linsum/window_secondnew.size();

angavg = angsum/window_secondnew.size();

그리고 가속도의 평균인 linavg와 회전 가속도의 평균인 angavg를 구해준다.

 

// Get z axis, which alines with -g (z_in_G=0,0,1)

Eigen::Vector3d z_axis = linavg/linavg.norm();

linavg는 하나의 vector이다. 

이러한 벡터가 존재할 때, Eigen::norm() 연산은 square root of dot production 을 통해 벡터의 길이를 구할 수 있게 해준다.

square root of the dot product

그리고 해당 벡터를 벡터의 길이로 나누게 되면 벡터를 정규화할 수 있게 되는 것이다.

여기서는 z축 벡터를 x축과 y축이 0인 벡터로 국한하지 않고, 기준이 되는 벡터로써 사용을 하는 것 같다.

 

// Create an x_axis

Eigen::Vector3d e_1(1,0,0);

x axis 에 대한 기저벡터를 만든다.

 

// Make x_axis perpendicular to z

Eigen::Vector3d x_axis = e_1-z_axis*z_axis.transpose()*e_1;

x_axis= x_axis/x_axis.norm();

transpose() 는 전치행렬을 만드는 함수이다.

 

x_axis를 z_axis에 수직으로 만드는 과정이라고 한다. 어떻게 진행되는지는 아직 모르겠다.

 

해당 부분에 대한 issue는 다음과 같다.

mathematical derivation of "initialize_with_imu()".

 

// Get z from the cross product of these two

Eigen::Matrix<double,3,1> y_axis = skew_x(z_axis)*x_axis;

ov_core::skew_x 는 주어진 벡터를 이용하여 비대칭 행렬을 만드는 함수이다.

다음과 같은 비대칭 행렬이 나오게 되며,

skew_symmetric matrix

이를 이용해 x_axis와 외적을 수행할 수 있다.

cross_product with skew_symmetric matrix

 

그렇다면 두 벡터의 외적은 무엇인가? 

두 벡터의 외적을 통해서 두 벡터에 공통으로 수직인 벡터를 구할 수 있게 되며, 

이 때, z축과 x축에 대해 수직인 벡터는 y축 이 되는 것이다.

 

// From these axes get rotation

Eigen::Matrix<double,3,3> Ro;

Ro.block(0,0,3,1) = x_axis;

Ro.block(0,1,3,1) = y_axis;

Ro.block(0,2,3,1) = z_axis;

구해진 값들은 이제 rotation 값이 되게 된다. (am으로부터 rotation을 구하게 되는건가?)

 

// Create our state variables

Eigen::Matrix<double,4,1> q_GtoI = rot_2_quat(Ro);

이를 quaternion 으로 바꾸어 준다.

 

// Set our biases equal to our noise (subtract our gravity from accelerometer bias)

Eigen::Matrix<double,3,1> bg = angavg;

Eigen::Matrix<double,3,1> ba = linavg - quat_2_Rot(q_GtoI)*_gravity;

구해주었던 angavg와 linavg 를 biases 로 set해준다.

 

// Set our state variables

time0 = window_secondnew.at(window_secondnew.size()-1).timestamp;

q_GtoI0 = q_GtoI;

b_w0 = bg;

v_I0inG = Eigen::Matrix<double,3,1>::Zero();

b_a0 = ba;

p_I0inG = Eigen::Matrix<double,3,1>::Zero();

구해준 값들을 파라미터들에 대입해준다.

 

// Done!!!

return true;

return 한다.

 

[IMU] state->_imu->set_value()

 

IMU 센서로부터 얻은 각 값들을 각 멤버변수에 담아준다.

 

해당 함수는 많은 부분에서 사용되므로 한번만 설명하고 넘어간다.

        /**
         * @brief Sets the value of the estimate
         * @param new_value New value we should set
         */
        void set_value(const Eigen::MatrixXd new_value) override {

            assert(new_value.rows() == 16);
            assert(new_value.cols() == 1);

            _pose->set_value(new_value.block(0, 0, 7, 1));
            _v->set_value(new_value.block(7, 0, 3, 1));
            _bg->set_value(new_value.block(10, 0, 3, 1));
            _ba->set_value(new_value.block(13, 0, 3, 1));

            _value = new_value;
        }

 

[Type::PoseJPL] _pose->set_value()

orientation value와 position valuse를 담는다.

        /**
         * @brief Sets the value of the estimate
         * @param new_value New value we should set
         */
        void set_value(const Eigen::MatrixXd new_value) override {

            assert(new_value.rows() == 7);
            assert(new_value.cols() == 1);

            //Set orientation value
            _q->set_value(new_value.block(0, 0, 4, 1));

            //Set position value
            _p->set_value(new_value.block(4, 0, 3, 1));

            _value = new_value;
        }

 

[Type::JPLQuat] _q->set_value()

quaternion을 _value에 저장하고,

해당 quaternion을 rotation matrix로 변환하여 _R에 저장한다.

 

해당 함수는 많은 부분에서 사용되므로 한번만 설명하고 넘어간다.

        /**
        * @brief Sets the value of the estimate and recomputes the internal rotation matrix
        * @param new_value New value for the quaternion estimate
        */
        void set_value(const Eigen::MatrixXd new_value) override {

            assert(new_value.rows() == 4);
            assert(new_value.cols() == 1);

            _value = new_value;

            //compute associated rotation
            _R = ov_core::quat_2_Rot(new_value);
        }

 

ov_core::quat_2_Rot()

quaternion을 rotation matrix로 바꿔주는 부분이다. 

자세한 내용은 차후에 확인하도록 하자.

 

20200713 내용 확인

 

어떠한 벡터 p가 있다고 하자.

 

이 때, Ground의 p를 local frame의 p로 회전시키는 행렬을 C라고 하자.

 quaternion을 사용해서 p를 외적하면 local frame으로 회전시킬 수 있다.

그리고 위 수식을 ground의 p 벡터에 대해 정리하면 다음과 같다.

 

 결국 최종적으로 다음의 회전행렬을 구할 수 있다.

 

해당내용을 구현한 함수이다.

 

    /**
     * @brief Converts JPL quaterion to SO(3) rotation matrix
     *
     * This is based on equation 62 in [Indirect Kalman Filter for 3D Attitude Estimation](http://mars.cs.umn.edu/tr/reports/Trawny05b.pdf):
     * \f{align*}{
     *  \mathbf{R} = (2q_4^2-1)\mathbf{I}_3-2q_4\lfloor\mathbf{q}\times\rfloor+2\mathbf{q}^\top\mathbf{q}
     * @f}
     *
     * @param[in] q JPL quaternion
     * @return 3x3 SO(3) rotation matrix
     */
    inline Eigen::Matrix<double, 3, 3> quat_2_Rot(const Eigen::Matrix<double, 4, 1> &q) {
        Eigen::Matrix<double, 3, 3> q_x = skew_x(q.block(0, 0, 3, 1));
        Eigen::MatrixXd Rot = (2 * std::pow(q(3, 0), 2) - 1) * Eigen::MatrixXd::Identity(3, 3)
                              - 2 * q(3, 0) * q_x +
                              2 * q.block(0, 0, 3, 1) * (q.block(0, 0, 3, 1).transpose());
        return Rot;
    }

 

[Type::Vec] _p->set_value()

아마 이건 Type 의 함수를 override 한 듯 하다.

 

해당 함수는 많은 부분에서 사용되므로 한번만 설명하고 넘어간다.

        /**
         * @brief Performs all the cloning
         */
        Type *clone() override {
            Type *Clone = new Vec(_size);
            Clone->set_value(value());
            Clone->set_fej(fej());
            return Clone;
        }


        /**
         * @brief Overwrite value of state's estimate
         * @param new_value New value that will overwrite state's value
         */
        virtual void set_value(const Eigen::MatrixXd new_value) {
            assert(_value.rows()==new_value.rows());
            assert(_value.cols()==new_value.cols());
            _value = new_value;
        }

 

 

[IMU] state->_imu->set_fej()

그냥 값 넣는거다. 위 내용과 크게 안다르다. 단지 각 변수에서 set_fej() 함수를 사용한다.

        /**
         * @brief Sets the value of the first estimate
         * @param new_value New value we should set
         */
        void set_fej(const Eigen::MatrixXd new_value) override {

            assert(new_value.rows() == 16);
            assert(new_value.cols() == 1);

            _pose->set_fej(new_value.block(0, 0, 7, 1));
            _v->set_fej(new_value.block(7, 0, 3, 1));
            _bg->set_fej(new_value.block(10, 0, 3, 1));
            _ba->set_fej(new_value.block(13, 0, 3, 1));

            _fej = new_value;
        }

 

[Type::PoseJPL] _pose->set_fej()

여기도 위와 크게 안다르다.

        /**
         * @brief Sets the value of the first estimate
         * @param new_value New value we should set
         */
        void set_fej(const Eigen::MatrixXd new_value) override {

            assert(new_value.rows() == 7);
            assert(new_value.cols() == 1);

            //Set orientation fej value
            _q->set_fej(new_value.block(0, 0, 4, 1));

            //Set position fej value
            _p->set_fej(new_value.block(4, 0, 3, 1));

            _fej = new_value;
        }

 

[Type::JPLQuat] _q->set_fej()

여기도 다른건 없다.

        /**
        * @brief Sets the fej value and recomputes the fej rotation matrix
        * @param new_value New value for the quaternion estimate
        */
        void set_fej(const Eigen::MatrixXd new_value) override {

            assert(new_value.rows() == 4);
            assert(new_value.cols() == 1);

            _fej = new_value;

            //compute associated rotation
            _Rfej = ov_core::quat_2_Rot(new_value);
        }

 

[Type::Vec] _p->set_fej()

여기도 다른게 없다.

        /**
         * @brief Performs all the cloning
         */
        Type *clone() override {
            Type *Clone = new Vec(_size);
            Clone->set_value(value());
            Clone->set_fej(fej());
            return Clone;
        }
        
                /**
         * @brief Overwrite value of first-estimate
         * @param new_value New value that will overwrite state's fej
         */
        virtual void set_fej(const Eigen::MatrixXd new_value) {
            assert(_fej.rows()==new_value.rows());
            assert(_fej.cols()==new_value.cols());
            _fej = new_value;
        }

 

 

 

 

clean_measurements()

        /**
         * @brief This function will delete all feature measurements that are older then the specified timestamp
         */
        void cleanup_measurements(double timestamp) {
            std::unique_lock<std::mutex> lck(mtx);
            for (auto it = features_idlookup.begin(); it != features_idlookup.end();) {
                // Remove the older measurements
                (*it).second->clean_older_measurements(timestamp);
                // Count how many measurements
                int ct_meas = 0;
                for(const auto &pair : (*it).second->timestamps) {
                    ct_meas += (*it).second->timestamps[pair.first].size();
                }
                // If delete flag is set, then delete it
                if (ct_meas < 1) {
                    delete (*it).second;
                    features_idlookup.erase(it++);
                } else {
                    it++;
                }
            }
        }

std::unique_lock<std::mutex> lck(mtx);

lock 해주기

 

for (auto it = features_idlookup.begin(); it != features_idlookup.end();) {

features_idlookup 에 대한 iterator를 이용한 반복문

 

// Remove the older measurements

(*it).second->clean_older_measurements(timestamp);

it 는 features_idlookup 을 의미하고 여기서 second 는 "Feat" 를 의미한다. 

Feat의 clean_older_measurements 함수를 수행하는 것이다.

이 때, timestamp를 매개변수로 쓰게 되는데 이는 현재 시간에 대한 정보이다.

 

// Count how many measurements

int ct_meas = 0;

for(const auto &pair : (*it).second->timestamps) {

ct_meas += (*it).second->timestamps[pair.first].size();

}

 

timestamps의 원형은 다음과 같다.

 

/// Timestamps of each UV measurement (mapped by camera ID)

std::unordered_map<size_t, std::vector<double>> timestamps;

 

그러므로 (*it).second->timestamps 를 반복문으로 돌린다는 것은 

unordered_map 을 대상으로 돌린다는 것이고,

stereo camera의 경우에는 2번 돌리겠지만,

mono camera의 경우에는 1번만 돌아갈 것이다.

 

size_t에는 camera ID가 들어가고 std::vector<double> 에는 time 들이 vector 형으로 기록되게 된다. 

 

이러한 timestamps 의 주소를 pair 로 가져오게 되는 것이고, 

pair.first 는 camera ID 가 되는 것이다. 

 

이러한 timestamps 안에 몇개의 데이터가 존재하는지를 카메라에 따른 평균을 내는 것이다.

 

// If delete flag is set, then delete it

if (ct_meas < 1) {

delete (*it).second;

features_idlookup.erase(it++);

} else {

it++;

}

만약 feature가 하나도 존재하지 않는다면, 해당 feature를 지워버리고 다음 feature로 넘어간다.

그렇지 않으면 바로 다음 feature로 넘어간다. 

 

 

clean_older_measurements()

initialize를 하기까지의 모든 measurements 들을 없애준다.

void Feature::clean_older_measurements(double timestamp) {


    // Loop through each of the cameras we have
    for(auto const &pair : timestamps) {

        // Assert that we have all the parts of a measurement
        assert(timestamps[pair.first].size() == uvs[pair.first].size());
        assert(timestamps[pair.first].size() == uvs_norm[pair.first].size());

        // Our iterators
        auto it1 = timestamps[pair.first].begin();
        auto it2 = uvs[pair.first].begin();
        auto it3 = uvs_norm[pair.first].begin();

        // Loop through measurement times, remove ones that are older then the specified one
        while (it1 != timestamps[pair.first].end()) {
            if (*it1 <= timestamp) {
                it1 = timestamps[pair.first].erase(it1);
                it2 = uvs[pair.first].erase(it2);
                it3 = uvs_norm[pair.first].erase(it3);
            } else {
                ++it1;
                ++it2;
                ++it3;
            }
        }
    }

}

 

VioManager::do_feature_propagate_update()

        /**
         * @brief This will do the propagation and feature updates to the state
         * @param timestamp The most recent timestamp we have tracked to
         */
        void do_feature_propagate_update(double timestamp);

void VioManager::do_feature_propagate_update(double timestamp) {


    //===================================================================================
    // State propagation, and clone augmentation
    //===================================================================================

    // Return if the camera measurement is out of order
    if(state->_timestamp >= timestamp) {
        printf(YELLOW "image received out of order (prop dt = %3f)\n" RESET,(timestamp-state->_timestamp));
        return;
    }

    // Propagate the state forward to the current update time
    // Also augment it with a new clone!
    propagator->propagate_and_clone(state, timestamp);
    rT3 =  boost::posix_time::microsec_clock::local_time();

    // If we have not reached max clones, we should just return...
    // This isn't super ideal, but it keeps the logic after this easier...
    // We can start processing things when we have at least 5 clones since we can start triangulating things...
    if((int)state->_clones_IMU.size() < std::min(state->_options.max_clone_size,5)) {
        printf("waiting for enough clone states (%d of %d)....\n",(int)state->_clones_IMU.size(),std::min(state->_options.max_clone_size,5));
        return;
    }

    // Return if we where unable to propagate
    if(state->_timestamp != timestamp) {
        printf(RED "[PROP]: Propagator unable to propagate the state forward in time!\n" RESET);
        printf(RED "[PROP]: It has been %.3f since last time we propagated\n" RESET,timestamp-state->_timestamp);
        return;
    }

    //===================================================================================
    // MSCKF features and KLT tracks that are SLAM features
    //===================================================================================


    // Now, lets get all features that should be used for an update that are lost in the newest frame
    std::vector<Feature*> feats_lost, feats_marg, feats_slam;
    feats_lost = trackFEATS->get_feature_database()->features_not_containing_newer(state->_timestamp);

    // Don't need to get the oldest features untill we reach our max number of clones
    if((int)state->_clones_IMU.size() > state->_options.max_clone_size) {
        feats_marg = trackFEATS->get_feature_database()->features_containing(state->margtimestep());
        if(trackARUCO != nullptr && timestamp-startup_time >= params.dt_slam_delay) {
            feats_slam = trackARUCO->get_feature_database()->features_containing(state->margtimestep());
        }
    }

    // We also need to make sure that the max tracks does not contain any lost features
    // This could happen if the feature was lost in the last frame, but has a measurement at the marg timestep
    auto it1 = feats_lost.begin();
    while(it1 != feats_lost.end()) {
        if(std::find(feats_marg.begin(),feats_marg.end(),(*it1)) != feats_marg.end()) {
            //printf(YELLOW "FOUND FEATURE THAT WAS IN BOTH feats_lost and feats_marg!!!!!!\n" RESET);
            it1 = feats_lost.erase(it1);
        } else {
            it1++;
        }
    }

    // Find tracks that have reached max length, these can be made into SLAM features
    std::vector<Feature*> feats_maxtracks;
    auto it2 = feats_marg.begin();
    while(it2 != feats_marg.end()) {
        // See if any of our camera's reached max track
        bool reached_max = false;
        for (const auto &cams: (*it2)->timestamps) {
            if ((int)cams.second.size() > state->_options.max_clone_size) {
                reached_max = true;
                break;
            }
        }
        // If max track, then add it to our possible slam feature list
        if(reached_max) {
            feats_maxtracks.push_back(*it2);
            it2 = feats_marg.erase(it2);
        } else {
            it2++;
        }
    }

    // Count how many aruco tags we have in our state
    int curr_aruco_tags = 0;
    auto it0 = state->_features_SLAM.begin();
    while(it0 != state->_features_SLAM.end()) {
        if ((int) (*it0).second->_featid <= state->_options.max_aruco_features) curr_aruco_tags++;
        it0++;
    }

    // Append a new SLAM feature if we have the room to do so
    // Also check that we have waited our delay amount (normally prevents bad first set of slam points)
    if(state->_options.max_slam_features > 0 && timestamp-startup_time >= params.dt_slam_delay && (int)state->_features_SLAM.size() < state->_options.max_slam_features+curr_aruco_tags) {
        // Get the total amount to add, then the max amount that we can add given our marginalize feature array
        int amount_to_add = (state->_options.max_slam_features+curr_aruco_tags)-(int)state->_features_SLAM.size();
        int valid_amount = (amount_to_add > (int)feats_maxtracks.size())? (int)feats_maxtracks.size() : amount_to_add;
        // If we have at least 1 that we can add, lets add it!
        // Note: we remove them from the feat_marg array since we don't want to reuse information...
        if(valid_amount > 0) {
            feats_slam.insert(feats_slam.end(), feats_maxtracks.end()-valid_amount, feats_maxtracks.end());
            feats_maxtracks.erase(feats_maxtracks.end()-valid_amount, feats_maxtracks.end());
        }
    }

    // Loop through current SLAM features, we have tracks of them, grab them for this update!
    // Note: if we have a slam feature that has lost tracking, then we should marginalize it out
    // Note: if you do not use FEJ, these types of slam features *degrade* the estimator performance....
    for (std::pair<const size_t, Landmark*> &landmark : state->_features_SLAM) {
        if(trackARUCO != nullptr) {
            Feature* feat1 = trackARUCO->get_feature_database()->get_feature(landmark.second->_featid);
            if(feat1 != nullptr) feats_slam.push_back(feat1);
        }
        Feature* feat2 = trackFEATS->get_feature_database()->get_feature(landmark.second->_featid);
        if(feat2 != nullptr) feats_slam.push_back(feat2);
        if(feat2 == nullptr) landmark.second->should_marg = true;
    }

    // Lets marginalize out all old SLAM features here
    // These are ones that where not successfully tracked into the current frame
    // We do *NOT* marginalize out our aruco tags
    StateHelper::marginalize_slam(state);

    // Separate our SLAM features into new ones, and old ones
    std::vector<Feature*> feats_slam_DELAYED, feats_slam_UPDATE;
    for(size_t i=0; i<feats_slam.size(); i++) {
        if(state->_features_SLAM.find(feats_slam.at(i)->featid) != state->_features_SLAM.end()) {
            feats_slam_UPDATE.push_back(feats_slam.at(i));
            //printf("[UPDATE-SLAM]: found old feature %d (%d measurements)\n",(int)feats_slam.at(i)->featid,(int)feats_slam.at(i)->timestamps_left.size());
        } else {
            feats_slam_DELAYED.push_back(feats_slam.at(i));
            //printf("[UPDATE-SLAM]: new feature ready %d (%d measurements)\n",(int)feats_slam.at(i)->featid,(int)feats_slam.at(i)->timestamps_left.size());
        }
    }

    // Concatenate our MSCKF feature arrays (i.e., ones not being used for slam updates)
    std::vector<Feature*> featsup_MSCKF = feats_lost;
    featsup_MSCKF.insert(featsup_MSCKF.end(), feats_marg.begin(), feats_marg.end());
    featsup_MSCKF.insert(featsup_MSCKF.end(), feats_maxtracks.begin(), feats_maxtracks.end());


    //===================================================================================
    // Now that we have a list of features, lets do the EKF update for MSCKF and SLAM!
    //===================================================================================


    // Pass them to our MSCKF updater
    // NOTE: if we have more then the max, we select the "best" ones (i.e. max tracks) for this update
    // NOTE: this should only really be used if you want to track a lot of features, or have limited computational resources
    if((int)featsup_MSCKF.size() > state->_options.max_msckf_in_update)
        featsup_MSCKF.erase(featsup_MSCKF.begin(), featsup_MSCKF.end()-state->_options.max_msckf_in_update);
    updaterMSCKF->update(state, featsup_MSCKF);
    rT4 =  boost::posix_time::microsec_clock::local_time();

    // Perform SLAM delay init and update
    // NOTE: that we provide the option here to do a *sequential* update
    // NOTE: this will be a lot faster but won't be as accurate.
    std::vector<Feature*> feats_slam_UPDATE_TEMP;
    while(!feats_slam_UPDATE.empty()) {
        // Get sub vector of the features we will update with
        std::vector<Feature*> featsup_TEMP;
        featsup_TEMP.insert(featsup_TEMP.begin(), feats_slam_UPDATE.begin(), feats_slam_UPDATE.begin()+std::min(state->_options.max_slam_in_update,(int)feats_slam_UPDATE.size()));
        feats_slam_UPDATE.erase(feats_slam_UPDATE.begin(), feats_slam_UPDATE.begin()+std::min(state->_options.max_slam_in_update,(int)feats_slam_UPDATE.size()));
        // Do the update
        updaterSLAM->update(state, featsup_TEMP);
        feats_slam_UPDATE_TEMP.insert(feats_slam_UPDATE_TEMP.end(), featsup_TEMP.begin(), featsup_TEMP.end());
    }
    feats_slam_UPDATE = feats_slam_UPDATE_TEMP;
    rT5 =  boost::posix_time::microsec_clock::local_time();
    updaterSLAM->delayed_init(state, feats_slam_DELAYED);
    rT6 =  boost::posix_time::microsec_clock::local_time();


    //===================================================================================
    // Update our visualization feature set, and clean up the old features
    //===================================================================================


    // Save all the MSCKF features used in the update
    good_features_MSCKF.clear();
    for(Feature* feat : featsup_MSCKF) {
        good_features_MSCKF.push_back(feat->p_FinG);
        feat->to_delete = true;
    }

    // Remove features that where used for the update from our extractors at the last timestep
    // This allows for measurements to be used in the future if they failed to be used this time
    // Note we need to do this before we feed a new image, as we want all new measurements to NOT be deleted
    trackFEATS->get_feature_database()->cleanup();
    if(trackARUCO != nullptr) {
        trackARUCO->get_feature_database()->cleanup();
    }

    //===================================================================================
    // Cleanup, marginalize out what we don't need any more...
    //===================================================================================

    // First do anchor change if we are about to lose an anchor pose
    updaterSLAM->change_anchors(state);

    // Marginalize the oldest clone of the state if we are at max length
    if((int)state->_clones_IMU.size() > state->_options.max_clone_size) {
        // Cleanup any features older then the marginalization time
        trackFEATS->get_feature_database()->cleanup_measurements(state->margtimestep());
        if(trackARUCO != nullptr) {
            trackARUCO->get_feature_database()->cleanup_measurements(state->margtimestep());
        }
        // Finally marginalize that clone
        StateHelper::marginalize_old_clone(state);
    }

    // Finally if we are optimizing our intrinsics, update our trackers
    if(state->_options.do_calib_camera_intrinsics) {
        // Get vectors arrays
        std::map<size_t, Eigen::VectorXd> cameranew_calib;
        std::map<size_t, bool> cameranew_fisheye;
        for(int i=0; i<state->_options.num_cameras; i++) {
            Vec* calib = state->_cam_intrinsics.at(i);
            bool isfish = state->_cam_intrinsics_model.at(i);
            cameranew_calib.insert({i,calib->value()});
            cameranew_fisheye.insert({i,isfish});
        }
        // Update the trackers and their databases
        trackFEATS->set_calibration(cameranew_calib, cameranew_fisheye, true);
        if(trackARUCO != nullptr) {
            trackARUCO->set_calibration(cameranew_calib, cameranew_fisheye, true);
        }
    }
    rT7 =  boost::posix_time::microsec_clock::local_time();


    //===================================================================================
    // Debug info, and stats tracking
    //===================================================================================

    // Get timing statitics information
    double time_track = (rT2-rT1).total_microseconds() * 1e-6;
    double time_prop = (rT3-rT2).total_microseconds() * 1e-6;
    double time_msckf = (rT4-rT3).total_microseconds() * 1e-6;
    double time_slam_update = (rT5-rT4).total_microseconds() * 1e-6;
    double time_slam_delay = (rT6-rT5).total_microseconds() * 1e-6;
    double time_marg = (rT7-rT6).total_microseconds() * 1e-6;
    double time_total = (rT7-rT1).total_microseconds() * 1e-6;

    // Timing information
    printf(BLUE "[TIME]: %.4f seconds for tracking\n" RESET, time_track);
    printf(BLUE "[TIME]: %.4f seconds for propagation\n" RESET, time_prop);
    printf(BLUE "[TIME]: %.4f seconds for MSCKF update (%d features)\n" RESET, time_msckf, (int)featsup_MSCKF.size());
    if(state->_options.max_slam_features > 0) {
        printf(BLUE "[TIME]: %.4f seconds for SLAM update (%d feats)\n" RESET, time_slam_update, (int)feats_slam_UPDATE.size());
        printf(BLUE "[TIME]: %.4f seconds for SLAM delayed init (%d feats)\n" RESET, time_slam_delay, (int)feats_slam_DELAYED.size());
    }
    printf(BLUE "[TIME]: %.4f seconds for marginalization (%d clones in state)\n" RESET, time_marg, (int)state->_clones_IMU.size());
    printf(BLUE "[TIME]: %.4f seconds for total\n" RESET, time_total);

    // Finally if we are saving stats to file, lets save it to file
    if(params.record_timing_information && of_statistics.is_open()) {
        // We want to publish in the IMU clock frame
        // The timestamp in the state will be the last camera time
        double t_ItoC = state->_calib_dt_CAMtoIMU->value()(0);
        double timestamp_inI = state->_timestamp + t_ItoC;
        // Append to the file
        of_statistics << std::fixed << std::setprecision(15)
                      << timestamp_inI << ","
                      << std::fixed << std::setprecision(5)
                      << time_track << "," << time_prop << "," << time_msckf << ",";
        if(state->_options.max_slam_features > 0) {
            of_statistics << time_slam_update << "," << time_slam_delay << ",";
        }
        of_statistics << time_marg << "," << time_total << std::endl;
        of_statistics.flush();
    }


    // Update our distance traveled
    if(timelastupdate != -1 && state->_clones_IMU.find(timelastupdate) != state->_clones_IMU.end()) {
        Eigen::Matrix<double,3,1> dx = state->_imu->pos() - state->_clones_IMU.at(timelastupdate)->pos();
        distance += dx.norm();
    }
    timelastupdate = timestamp;

    // Debug, print our current state
    printf("q_GtoI = %.3f,%.3f,%.3f,%.3f | p_IinG = %.3f,%.3f,%.3f | dist = %.2f (meters)\n",
            state->_imu->quat()(0),state->_imu->quat()(1),state->_imu->quat()(2),state->_imu->quat()(3),
            state->_imu->pos()(0),state->_imu->pos()(1),state->_imu->pos()(2),distance);
    printf("bg = %.4f,%.4f,%.4f | ba = %.4f,%.4f,%.4f\n",
             state->_imu->bias_g()(0),state->_imu->bias_g()(1),state->_imu->bias_g()(2),
             state->_imu->bias_a()(0),state->_imu->bias_a()(1),state->_imu->bias_a()(2));


    // Debug for camera imu offset
    if(state->_options.do_calib_camera_timeoffset) {
        printf("camera-imu timeoffset = %.5f\n",state->_calib_dt_CAMtoIMU->value()(0));
    }

    // Debug for camera intrinsics
    if(state->_options.do_calib_camera_intrinsics) {
        for(int i=0; i<state->_options.num_cameras; i++) {
            Vec* calib = state->_cam_intrinsics.at(i);
            printf("cam%d intrinsics = %.3f,%.3f,%.3f,%.3f | %.3f,%.3f,%.3f,%.3f\n",(int)i,
                     calib->value()(0),calib->value()(1),calib->value()(2),calib->value()(3),
                     calib->value()(4),calib->value()(5),calib->value()(6),calib->value()(7));
        }
    }

    // Debug for camera extrinsics
    if(state->_options.do_calib_camera_pose) {
        for(int i=0; i<state->_options.num_cameras; i++) {
            PoseJPL* calib = state->_calib_IMUtoCAM.at(i);
            printf("cam%d extrinsics = %.3f,%.3f,%.3f,%.3f | %.3f,%.3f,%.3f\n",(int)i,
                     calib->quat()(0),calib->quat()(1),calib->quat()(2),calib->quat()(3),
                     calib->pos()(0),calib->pos()(1),calib->pos()(2));
        }
    }


}

//===================================================================================

// State propagation, and clone augmentation

//===================================================================================

// Return if the camera measurement is out of order

if(state->_timestamp >= timestamp) {

printf(YELLOW "image received out of order (prop dt = %3f)\n" RESET,(timestamp-state->_timestamp));

return;

}

현재 state의 timestamp가 마지막 state의 timestamp보다 작다면 에러를 출력하고 return한다.

 

// Propagate the state forward to the current update time

// Also augment it with a new clone!

propagator->propagate_and_clone(state, timestamp);

rT3 = boost::posix_time::microsec_clock::local_time();

imu data에 대해 propagate를 진행하고 imu pose를 clone한다. 이는 state->_IMU_CLONES에 저장된다.

 

// Return if we where unable to propagate

if(state->_timestamp != timestamp) {

printf(RED "[PROP]: Propagator unable to propagate the state forward in time!\n" RESET);

printf(RED "[PROP]: It has been %.3f since last time we propagated\n" RESET,timestamp-state->_timestamp);

return;

}

state의 마지막 timestamp가 현재 state의 timestamp와 일치하지 않는다면 연산이 정상적으로 이루어지지 않은 것이므로 return 한다.

 

//===================================================================================

// MSCKF features and KLT tracks that are SLAM features

//===================================================================================

// Now, lets get all features that should be used for an update that are lost in the newest frame

std::vector<Feature*> feats_lost, feats_marg, feats_slam;

feats_lost = trackFEATS->get_feature_database()->features_not_containing_newer(state->_timestamp);

먼저 새로운 프레임에 포함되지 않는 오래된 features 를 가져와 feats_lost에 담아준다.

 

// Don't need to get the oldest features untill we reach our max number of clones

if((int)state->_clones_IMU.size() > state->_options.max_clone_size) {

feats_marg = trackFEATS->get_feature_database()->features_containing(state->margtimestep());

if(trackARUCO != nullptr && timestamp-startup_time >= params.dt_slam_delay) {

feats_slam = trackARUCO->get_feature_database()->features_containing(state->margtimestep());

}

}

만일 우리의 IMU clone이 초기 설정 파라미터인 max_clone_size 보다 크다면 조건문이 작동한다.

 

features_containing() 은 파라미터로 주어지는 시간에 해당하는 feature를 반환하며,

state->margtimestep()은 marginalize할 시간을 반환하는데, 현재 시스템에서는 imu clone 데이터들 중 가장 오래된 데이터의 시간이 된다.

 

즉 가장 오래된 imu clone에 대한 feature 데이터를 받아오는 것이다.

 

// We also need to make sure that the max tracks does not contain any lost features

// This could happen if the feature was lost in the last frame, but has a measurement at the marg timestep

auto it1 = feats_lost.begin();

while(it1 != feats_lost.end()) {

if(std::find(feats_marg.begin(),feats_marg.end(),(*it1)) != feats_marg.end()) {

//printf(YELLOW "FOUND FEATURE THAT WAS IN BOTH feats_lost and feats_marg!!!!!!\n" RESET);

it1 = feats_lost.erase(it1);

} else {

it1++;

}

}

unordered_map은 hash_map 구조를 갖는 데이터 형이며,

key와 value 값을 갖는 데이터들을 빠르게 검색할 수 있다는 특징을 지닌다.

 

std::unordered_map::find 함수는 파라미터로 주어지는 key 값을 찾는 iterator이며,

해당 key 값을 찾았을 때는 해당 key 값과 매칭되는 value를 반환하게 되고, 찾지 못했을 경우는
std::unordered_map::end 를 반환하게 된다. 

 

if(std::find(feats_marg.begin(),feats_marg.end(),(*it1)) != feats_marg.end()) 는

key 값이 존재하는 경우에 작동하는 조건문이라고 보면 된다.

 

즉, feats_lost의 feature 중 feats_marg와 겹치는 feature가 존재한다면.

feats_lost에서 지워주게 되는 것이다.

 

이 때, feats_marg가 가장 오래된 imu clone과 매칭되는 feature이므로,

last frame 에서 얻은 feats_lost 중 가장 오래된 feature인 feature marg와 겹치는 것이 있다면 feature_lost 에서 지워줌으로써 어찌보면 없애지 않는다? 라고 보면 될 것 같다. 

 

// Find tracks that have reached max length, these can be made into SLAM features

std::vector<Feature*> feats_maxtracks;

auto it2 = feats_marg.begin();

while(it2 != feats_marg.end()) {

// See if any of our camera's reached max track

bool reached_max = false;

for (const auto &cams: (*it2)->timestamps) {

if ((int)cams.second.size() > state->_options.max_clone_size) {

reached_max = true;

break;

}

}

// If max track, then add it to our possible slam feature list

if(reached_max) {

feats_maxtracks.push_back(*it2);

it2 = feats_marg.erase(it2);

} else {

it2++;

}

}

max_clone_size 보다 많은 feature를 가지고 있다면, SLAM feature를 만들 가능성이 있기 때문에,

가장 오래된 feature인 feats_marg 의 feature들을 feats_maxtracks에 담아줌으로써 SLAM features에 대한 후보군을 만들어준다.

 

// Count how many aruco tags we have in our state

int curr_aruco_tags = 0;

auto it0 = state->_features_SLAM.begin();

while(it0 != state->_features_SLAM.end()) {

if ((int) (*it0).second->_featid <= state->_options.max_aruco_features) curr_aruco_tags++;

it0++;

}

우린 aruco tags는 다루지 않으니 패스한다.

 

// Append a new SLAM feature if we have the room to do so

// Also check that we have waited our delay amount (normally prevents bad first set of slam points)

if(state->_options.max_slam_features > 0 && timestamp-startup_time >= params.dt_slam_delay && (int)state->_features_SLAM.size() < state->_options.max_slam_features+curr_aruco_tags) {

이제 SLAM feature를 만들게 된다. 

그리고 delay amount를 체크함으로써 bad first set of slam points를 예방한다.

조건은 다음과 같다.

1. 초기 설정 파라미터인 max_slam_features가 0보다 크다.

2. timestamp-startup_time 시간이 초기 설정 파라미터인 dt_slam_delay 보다는 커야한다. (정확도를 높이기 위해 해당 값을 늘려보아야 겠다. 하지만 너무 늘리면 slam features를 만드는데 시간이 오래 걸릴 것이다.)

3.  max_slam_features 파라미터 값보다 우리가 갖고있는 _features_SLAM의 값이 작아야 한다. ( 이 값을 늘리면 정확도가 높아질까? 큰 상관은 없을 듯 하다. 왜냐하면 slam features가 많이 검출되지는 않기 때문이다.)

 

// Get the total amount to add, then the max amount that we can add given our marginalize feature array

int amount_to_add = (state->_options.max_slam_features+curr_aruco_tags)-(int)state->_features_SLAM.size();

int valid_amount = (amount_to_add > (int)feats_maxtracks.size())? (int)feats_maxtracks.size() : amount_to_add;

우리가 추가할 수 있는 SLAM feature의 양을 구한다. 

amount_to_add의 양이 feats_marg에서 발견된 features보다 크다면 feats_maxtracks.size()가 valid_amount가 되고,

반대의 경우, amount_to_add가 valid_amount가 된다.  단순한 연산이다.

 

// If we have at least 1 that we can add, lets add it!

// Note: we remove them from the feat_marg array since we don't want to reuse information...

if(valid_amount > 0) {

feats_slam.insert(feats_slam.end(), feats_maxtracks.end()-valid_amount, feats_maxtracks.end());

feats_maxtracks.erase(feats_maxtracks.end()-valid_amount, feats_maxtracks.end());

}

이제 feats_slam에 feats_marg로부터 얻은 features를 가능한 만큼 담아주고, 

feats_maxtracks에서는 삭제해준다.

 

vector의 insert에 iterator를 사용하는 경우, 다음과 같이 생각하면 된다.

 

iterator insert (const_iterator position, InputIterator first, InputIterator last);

 

즉, 첫번째 인자는 iterator의 값들을 insert할 주소이고,

두번째 인자는 iterator를 시작할 주소,

세번째 인자는 iterator를 끝낼 주소가 된다.

 

// Loop through current SLAM features, we have tracks of them, grab them for this update!

// Note: if we have a slam feature that has lost tracking, then we should marginalize it out

// Note: if you do not use FEJ, these types of slam features *degrade* the estimator performance....

for (std::pair<const size_t, Landmark*> &landmark : state->_features_SLAM) {

if(trackARUCO != nullptr) {

Feature* feat1 = trackARUCO->get_feature_database()->get_feature(landmark.second->_featid);

if(feat1 != nullptr) feats_slam.push_back(feat1);

}

Feature* feat2 = trackFEATS->get_feature_database()->get_feature(landmark.second->_featid);

if(feat2 != nullptr) feats_slam.push_back(feat2);

if(feat2 == nullptr) landmark.second->should_marg = true;

}

우리 _features_SLAM에 존재하는 landmark의 _featid를 가져와 track된 feature인 trackFEATS 객체안의 특징점 정보를 검색하여 landmark의 _featid와 동일한 id를 갖는 feature가 존재한다면 feats_slam에 넣어준다.

landmark의 _featid와 동일한 id를 갖는 feature가 존재하지 않는다면, features_SLAM에서 marginalization 하기 위해 should_marg를 true로 해준다.

 

// Lets marginalize out all old SLAM features here

// These are ones that where not successfully tracked into the current frame

// We do *NOT* marginalize out our aruco tags

StateHelper::marginalize_slam(state);

여기서 current frame을 tracking 하지 못한 _features_SLAM 들을 marginalize 한다.

즉, landmark에 해당하지 않는 feature들은 지워준다.

 

// Separate our SLAM features into new ones, and old ones

std::vector<Feature*> feats_slam_DELAYED, feats_slam_UPDATE;

for(size_t i=0; i<feats_slam.size(); i++) {

if(state->_features_SLAM.find(feats_slam.at(i)->featid) != state->_features_SLAM.end()) {

feats_slam_UPDATE.push_back(feats_slam.at(i));

//printf("[UPDATE-SLAM]: found old feature %d (%d measurements)\n",(int)feats_slam.at(i)->featid,(int)feats_slam.at(i)->timestamps_left.size());

} else {

feats_slam_DELAYED.push_back(feats_slam.at(i));

//printf("[UPDATE-SLAM]: new feature ready %d (%d measurements)\n",(int)feats_slam.at(i)->featid,(int)feats_slam.at(i)->timestamps_left.size());

}

}

새로 얻은 feats_slam의 features(가장 오래된 features들 중 landmark가 존재하는 features) 중에 기존의 state->_features_SLAM과 같은 녀석이 있다면 feats_slam_UPDATE에 담아주고, 그렇지 않은 녀석들은 feats_slam_DELAYED에 담아준다.

 

// Concatenate our MSCKF feature arrays (i.e., ones not being used for slam updates)

std::vector<Feature*> featsup_MSCKF = feats_lost;

featsup_MSCKF.insert(featsup_MSCKF.end(), feats_marg.begin(), feats_marg.end());

featsup_MSCKF.insert(featsup_MSCKF.end(), feats_maxtracks.begin(), feats_maxtracks.end());

SLAM updates에 사용되지 않았던 녀석들은 featsup_MSCKF에 담아준다.

 

//===================================================================================

// Now that we have a list of features, lets do the EKF update for MSCKF and SLAM!

//===================================================================================

이제 위에서 구한 feature 정보들을 이용해 EKF update를 진행하게 된다.

 

// Pass them to our MSCKF updater

// NOTE: if we have more then the max, we select the "best" ones (i.e. max tracks) for this update

// NOTE: this should only really be used if you want to track a lot of features, or have limited computational resources

if((int)featsup_MSCKF.size() > state->_options.max_msckf_in_update)

featsup_MSCKF.erase(featsup_MSCKF.begin(), featsup_MSCKF.end()-state->_options.max_msckf_in_update);

 먼저 초기 설정 파라미터인 max_msckf_in_update 보다 앞의 과정에서 얻은 landmark에 해당하지 않는 feature들인 featsup_MSCKF의 개수가 많은지 확인한 후, max_msckf_in_update 만큼 지워준다.

 

updaterMSCKF->update(state, featsup_MSCKF);

 featsup_MSCKF를 업데이트 한다.

 

rT4 = boost::posix_time::microsec_clock::local_time();

 시간측정용이다.

 

while(!feats_slam_UPDATE.empty()) {

// Get sub vector of the features we will update with

std::vector<Feature*> featsup_TEMP;

featsup_TEMP.insert(featsup_TEMP.begin(), feats_slam_UPDATE.begin(), feats_slam_UPDATE.begin()+std::min(state->_options.max_slam_in_update,(int)feats_slam_UPDATE.size()));

feats_slam_UPDATE.erase(feats_slam_UPDATE.begin(), feats_slam_UPDATE.begin()+std::min(state->_options.max_slam_in_update,(int)feats_slam_UPDATE.size()));

// Do the update

updaterSLAM->update(state, featsup_TEMP);

feats_slam_UPDATE_TEMP.insert(feats_slam_UPDATE_TEMP.end(), featsup_TEMP.begin(), featsup_TEMP.end());

}

 앞의 과정에서 얻었던 새로 얻은 feats_slam의 features(가장 오래된 features들 중 landmark가 존재하는 features) 중에 기존의 state->_features_SLAM과 같은 features인 feats_slam_UPDATE를 가져와 max_slam_in_update의 개수만큼 featsup_TEMP에 담아주고, feats_slam_UPDATE에서는 지워준다. 

이 후에 featsup_TEMP를 updaterSLAM에 update 해준다.

 

vector의 insert에 iterator를 사용하는 경우, 다음과 같이 생각하면 된다.

 

iterator insert (const_iterator position, InputIterator first, InputIterator last);

 

즉, 첫번째 인자는 iterator의 값들을 insert할 주소이고,

두번째 인자는 iterator를 시작할 주소,

세번째 인자는 iterator를 끝낼 주소가 된다.

 

즉, feats_slam_UPDATE_TEMP에 featsup_TEMP 의 데이터를 추가하게 되는 것이다.

 

// Collect all slam features into single vector

std::vector<Feature*> features_used_in_update = featsup_MSCKF;

features_used_in_update.insert(features_used_in_update.end(), feats_slam_UPDATE.begin(), feats_slam_UPDATE.end());

features_used_in_update.insert(features_used_in_update.end(), feats_slam_DELAYED.begin(), feats_slam_DELAYED.end());

update_keyframe_historical_information(features_used_in_update);

이제 지금까지 사용했던 features 정보들을 features_used_in_update에 담아

update_keyframe_historical_information() 함수의 파라미터로 넣는다.

update_keyframe_historical_information() 는 지금까지 tracking한 정보들 중 최적의 정보만을 수집하게 된다.

 

// Save all the MSCKF features used in the update

good_features_MSCKF.clear();

for(Feature* feat : featsup_MSCKF) {

good_features_MSCKF.push_back(feat->p_FinG);

feat->to_delete = true;

}

이제 good_features_MSCKF에 featsup_MSCKF 정보를 담는다.

그리고 featsup_MSCKF의 features를 삭제할 수 있도록 feat->to_delete를 true로 만들어준다.

 

// Remove features that where used for the update from our extractors at the last timestep

// This allows for measurements to be used in the future if they failed to be used this time

// Note we need to do this before we feed a new image, as we want all new measurements to NOT be deleted

trackFEATS->get_feature_database()->cleanup();

 이제 기존에 갖고있던 features 들을 모두 지워준다.

 

//===================================================================================

// Cleanup, marginalize out what we don't need any more...

//===================================================================================

 

// First do anchor change if we are about to lose an anchor pose

updaterSLAM->change_anchors(state);

 anchor frame을 변경해준다.

 

// Cleanup any features older then the marginalization time

trackFEATS->get_feature_database()->cleanup_measurements(state->margtimestep());

 marginalize time 보다 오래된 features 들을 제거해준다.

 

// Finally marginalize the oldest clone if needed

StateHelper::marginalize_old_clone(state);

 marginalize 보다 오래된 clone 들을 제거해준다.

 

 

 

 

 

 

 

 

 

 

propagator->propagate_and_clone()

        /**
         * @brief Propagate state up to given timestamp and then clone
         *
         * This will first collect all imu readings that occured between the
         * *current* state time and the new time we want the state to be at.
         * If we don't have any imu readings we will try to extrapolate into the future.
         * After propagating the mean and covariance using our dynamics,
         * We clone the current imu pose as a new clone in our state.
         *
         * @param state Pointer to state
         * @param timestamp Time to propagate to and clone at
         */
        void propagate_and_clone(State *state, double timestamp);
        
        void Propagator::propagate_and_clone(State* state, double timestamp) {

    // If the difference between the current update time and state is zero
    // We should crash, as this means we would have two clones at the same time!!!!
    if(state->_timestamp == timestamp) {
        printf(RED "Propagator::propagate_and_clone(): Propagation called again at same timestep at last update timestep!!!!\n" RESET);
        std::exit(EXIT_FAILURE);
    }

    // We should crash if we are trying to propagate backwards
    if(state->_timestamp > timestamp) {
        printf(RED "Propagator::propagate_and_clone(): Propagation called trying to propagate backwards in time!!!!\n" RESET);
        printf(RED "Propagator::propagate_and_clone(): desired propagation = %.4f\n" RESET, (timestamp-state->_timestamp));
        std::exit(EXIT_FAILURE);
    }

    //===================================================================================
    //===================================================================================
    //===================================================================================

    // Set the last time offset value if we have just started the system up
    if(!have_last_prop_time_offset) {
        last_prop_time_offset = state->_calib_dt_CAMtoIMU->value()(0);
        have_last_prop_time_offset = true;
    }

    // Get what our IMU-camera offset should be (t_imu = t_cam + calib_dt)
    double t_off_new = state->_calib_dt_CAMtoIMU->value()(0);

    // First lets construct an IMU vector of measurements we need
    double time0 = state->_timestamp+last_prop_time_offset;
    double time1 = timestamp+t_off_new;
    vector<IMUDATA> prop_data = Propagator::select_imu_readings(imu_data,time0,time1);

    // We are going to sum up all the state transition matrices, so we can do a single large multiplication at the end
    // Phi_summed = Phi_i*Phi_summed
    // Q_summed = Phi_i*Q_summed*Phi_i^T + Q_i
    // After summing we can multiple the total phi to get the updated covariance
    // We will then add the noise to the IMU portion of the state
    Eigen::Matrix<double,15,15> Phi_summed = Eigen::Matrix<double,15,15>::Identity();
    Eigen::Matrix<double,15,15> Qd_summed = Eigen::Matrix<double,15,15>::Zero();
    double dt_summed = 0;

    // Loop through all IMU messages, and use them to move the state forward in time
    // This uses the zero'th order quat, and then constant acceleration discrete
    if(prop_data.size() > 1) {
        for(size_t i=0; i<prop_data.size()-1; i++) {

            // Get the next state Jacobian and noise Jacobian for this IMU reading
            Eigen::Matrix<double, 15, 15> F = Eigen::Matrix<double, 15, 15>::Zero();
            Eigen::Matrix<double, 15, 15> Qdi = Eigen::Matrix<double, 15, 15>::Zero();
            predict_and_compute(state, prop_data.at(i), prop_data.at(i+1), F, Qdi);

            // Next we should propagate our IMU covariance
            // Pii' = F*Pii*F.transpose() + G*Q*G.transpose()
            // Pci' = F*Pci and Pic' = Pic*F.transpose()
            // NOTE: Here we are summing the state transition F so we can do a single mutiplication later
            // NOTE: Phi_summed = Phi_i*Phi_summed
            // NOTE: Q_summed = Phi_i*Q_summed*Phi_i^T + G*Q_i*G^T
            Phi_summed = F * Phi_summed;
            Qd_summed = F * Qd_summed * F.transpose() + Qdi;
            Qd_summed = 0.5*(Qd_summed+Qd_summed.transpose());
            dt_summed +=  prop_data.at(i+1).timestamp-prop_data.at(i).timestamp;
        }
    }

    // Last angular velocity (used for cloning when estimating time offset)
    Eigen::Matrix<double,3,1> last_w = Eigen::Matrix<double,3,1>::Zero();
    if(prop_data.size() > 1) last_w = prop_data.at(prop_data.size()-2).wm - state->_imu->bias_g();
    else if(!prop_data.empty()) last_w = prop_data.at(prop_data.size()-1).wm - state->_imu->bias_g();

    // Do the update to the covariance with our "summed" state transition and IMU noise addition...
    std::vector<Type*> Phi_order;
    Phi_order.push_back(state->_imu);
    StateHelper::EKFPropagation(state, Phi_order, Phi_order, Phi_summed, Qd_summed);

    // Set timestamp data
    state->_timestamp = timestamp;
    last_prop_time_offset = t_off_new;

    // Now perform stochastic cloning
    StateHelper::augment_clone(state, last_w);

}

// If the difference between the current update time and state is zero

// We should crash, as this means we would have two clones at the same time!!!!

if(state->_timestamp == timestamp) {

printf(RED "Propagator::propagate_and_clone(): Propagation called again at same timestep at last update timestep!!!!\n" RESET);

std::exit(EXIT_FAILURE);

}

최근 imu data의 timestamp와 현재 imu data의 imestamp가 같다면 중복되는 문제가 생기므로 에러를 체크한다.

 

// We should crash if we are trying to propagate backwards

if(state->_timestamp > timestamp) {

printf(RED "Propagator::propagate_and_clone(): Propagation called trying to propagate backwards in time!!!!\n" RESET);

printf(RED "Propagator::propagate_and_clone(): desired propagation = %.4f\n" RESET, (timestamp-state->_timestamp));

std::exit(EXIT_FAILURE);

}

만약 현재 작업하려는 imu data의 timestamp가 최근 imu data의 imestamp보다 일찍 생성되었다면 거꾸로 propagation이 진행되는 것이니 이것도 체크한다.

 

// Set the last time offset value if we have just started the system up

if(!have_last_prop_time_offset) {

last_prop_time_offset = state->_calib_dt_CAMtoIMU->value()(0);

have_last_prop_time_offset = true;

}

만약 우리가 propagate를 처음 시작했다면, 초기 파라미터 설정에서 calibration dt 값을 가져와서 last_prop_time_offset 값으로 만들어주고 have_last_prop_time_offset 파라미터를 true로 만들어준다.

 

// Get what our IMU-camera offset should be (t_imu = t_cam + calib_dt)

double t_off_new = state->_calib_dt_CAMtoIMU->value()(0);

일단 초기 파라미터 설정에서 camera와 imu의 time_offset을 가져온다.

 

// First lets construct an IMU vector of measurements we need

double time0 = state->_timestamp+last_prop_time_offset;

double time1 = timestamp+t_off_new;

vector<IMUDATA> prop_data = Propagator::select_imu_readings(imu_data,time0,time1);

time0의 경우 최근 state의 timestamp에 마지막 propagation의 time offset을 더한 값이고,

time1의 경우 현재 timestamp 값에 camera와 imu 간의 time offset 값을 더한 값이다.

imu data와 time0, time1을 select_imu_readings() 함수에 파라미터로 주어 interval 사이의 적절한 imu data만을 선정한다.

 

// We are going to sum up all the state transition matrices, so we can do a single large multiplication at the end

// Phi_summed = Phi_i*Phi_summed

// Q_summed = Phi_i*Q_summed*Phi_i^T + Q_i

// After summing we can multiple the total phi to get the updated covariance

// We will then add the noise to the IMU portion of the state

Eigen::Matrix<double,15,15> Phi_summed = Eigen::Matrix<double,15,15>::Identity();

Eigen::Matrix<double,15,15> Qd_summed = Eigen::Matrix<double,15,15>::Zero();

double dt_summed = 0;

이제 누적된 transition matrix인 Phi_summed와

누적된 covariance matrix인 Q_summed를 선언한다.

누적된 시간인 dt_summed도 선언한다.

 

// Loop through all IMU messages, and use them to move the state forward in time

// This uses the zero'th order quat, and then constant acceleration discrete

if(prop_data.size() > 1) {

for(size_t i=0; i<prop_data.size()-1; i++) {

이제 interval간에 imu_data들을 이용해서 state를 이동시키기 위해 반복문을 수행한다.

 

// Get the next state Jacobian and noise Jacobian for this IMU reading

Eigen::Matrix<double, 15, 15> F = Eigen::Matrix<double, 15, 15>::Zero();

Eigen::Matrix<double, 15, 15> Qdi = Eigen::Matrix<double, 15, 15>::Zero();

predict_and_compute(state, prop_data.at(i), prop_data.at(i+1), F, Qdi);

두 imu data 간에 system jacobian matrix인 F와 covariance matrix인 Qdi를 구한다.

이 때, predict_and_compute() 함수를 사용한다.

 

// Next we should propagate our IMU covariance

// Pii' = F*Pii*F.transpose() + G*Q*G.transpose()

// Pci' = F*Pci and Pic' = Pic*F.transpose()

// NOTE: Here we are summing the state transition F so we can do a single mutiplication later

// NOTE: Phi_summed = Phi_i*Phi_summed

// NOTE: Q_summed = Phi_i*Q_summed*Phi_i^T + G*Q_i*G^T

Phi_summed = F * Phi_summed;

Qd_summed = F * Qd_summed * F.transpose() + Qdi;

Qd_summed = 0.5*(Qd_summed+Qd_summed.transpose());

dt_summed += prop_data.at(i+1).timestamp-prop_data.at(i).timestamp;

여기서 우리는 위의 수식을 얻기위한 사전 작업을 수행한다.

먼저 위의 predict_and_compute() 함수를 통해서 G*Q_i*G^T는 얻어온 상태이다.

 

일단은 추후의 single multiplication을 위해 Phi_summed를 transition F 와 곱해준다.

그리고 위의 수식을 통해 Qd_summed(P(k+1, k))를 얻어준다.

그리고 propagation에 걸린 시간을 dt_summed에 더해준다.

 

// Last angular velocity (used for cloning when estimating time offset)

Eigen::Matrix<double,3,1> last_w = Eigen::Matrix<double,3,1>::Zero();

if(prop_data.size() > 1) last_w = prop_data.at(prop_data.size()-2).wm - state->_imu->bias_g();

else if(!prop_data.empty()) last_w = prop_data.at(prop_data.size()-1).wm - state->_imu->bias_g();

imu data의 마지막 회전 데이터를 가져와서 마지막 회전 속도를 구해준다.

이 값은 추후에cloning을 위해 time offset을 추정할 때 쓰인다.

 

// Do the update to the covariance with our "summed" state transition and IMU noise addition...

std::vector<Type*> Phi_order;

Phi_order.push_back(state->_imu);

StateHelper::EKFPropagation(state, Phi_order, Phi_order, Phi_summed, Qd_summed);

이제 EKFPropagation을 통해 state의 covariance에 현재까지 합쳐진 transition과 IMU noise를 추가해준다. 

 

// Set timestamp data

state->_timestamp = timestamp;

last_prop_time_offset = t_off_new;

이제 state의 _timestamp를 현재 timestamp로 바꾸어준다.

이제 마지막 propagation time offset을 바꾸어준다.

 

// Now perform stochastic cloning

StateHelper::augment_clone(state, last_w);

이제 통계적으로 clone을 진행한다.

 

 

 

selsect_imu_reading()

        /**
         * @brief Helper function that given current imu data, will select imu readings between the two times.
         *
         * This will create measurements that we will integrate with, and an extra measurement at the end.
         * We use the @ref interpolate_data() function to "cut" the imu readings at the begining and end of the integration.
         * The timestamps passed should already take into account the time offset values.
         *
         * @param imu_data IMU data we will select measurements from
         * @param time0 Start timestamp
         * @param time1 End timestamp
         * @return Vector of measurements (if we could compute them)
         */
        static std::vector<IMUDATA> select_imu_readings(const std::vector<IMUDATA>& imu_data, double time0, double time1);
        
        
std::vector<Propagator::IMUDATA> Propagator::select_imu_readings(const std::vector<IMUDATA>& imu_data, double time0, double time1) {

    // Our vector imu readings
    std::vector<Propagator::IMUDATA> prop_data;

    // Ensure we have some measurements in the first place!
    if(imu_data.empty()) {
        printf(YELLOW "Propagator::select_imu_readings(): No IMU measurements. IMU-CAMERA are likely messed up!!!\n" RESET);
        return prop_data;
    }

    // Loop through and find all the needed measurements to propagate with
    // Note we split measurements based on the given state time, and the update timestamp
    for(size_t i=0; i<imu_data.size()-1; i++) {

        // START OF THE INTEGRATION PERIOD
        // If the next timestamp is greater then our current state time
        // And the current is not greater then it yet...
        // Then we should "split" our current IMU measurement
        if(imu_data.at(i+1).timestamp > time0 && imu_data.at(i).timestamp < time0) {
            IMUDATA data = Propagator::interpolate_data(imu_data.at(i),imu_data.at(i+1), time0);
            prop_data.push_back(data);
            //printf("propagation #%d = CASE 1 = %.3f => %.3f\n", (int)i,data.timestamp-prop_data.at(0).timestamp,time0-prop_data.at(0).timestamp);
            continue;
        }

        // MIDDLE OF INTEGRATION PERIOD
        // If our imu measurement is right in the middle of our propagation period
        // Then we should just append the whole measurement time to our propagation vector
        if(imu_data.at(i).timestamp >= time0 && imu_data.at(i+1).timestamp <= time1) {
            prop_data.push_back(imu_data.at(i));
            //printf("propagation #%d = CASE 2 = %.3f\n",(int)i,imu_data.at(i).timestamp-prop_data.at(0).timestamp);
            continue;
        }

        // END OF THE INTEGRATION PERIOD
        // If the current timestamp is greater then our update time
        // We should just "split" the NEXT IMU measurement to the update time,
        // NOTE: we add the current time, and then the time at the end of the interval (so we can get a dt)
        // NOTE: we also break out of this loop, as this is the last IMU measurement we need!
        if(imu_data.at(i+1).timestamp > time1) {
            // If we have a very low frequency IMU then, we could have only recorded the first integration (i.e. case 1) and nothing else
            // In this case, both the current IMU measurement and the next is greater than the desired intepolation, thus we should just cut the current at the desired time
            // Else, we have hit CASE2 and this IMU measurement is not past the desired propagation time, thus add the whole IMU reading
            if(imu_data.at(i).timestamp > time1) {
                IMUDATA data = interpolate_data(imu_data.at(i-1), imu_data.at(i), time1);
                prop_data.push_back(data);
                //printf("propagation #%d = CASE 3.1 = %.3f => %.3f\n", (int)i,imu_data.at(i).timestamp-prop_data.at(0).timestamp,imu_data.at(i).timestamp-time0);
            } else {
                prop_data.push_back(imu_data.at(i));
                //printf("propagation #%d = CASE 3.2 = %.3f => %.3f\n", (int)i,imu_data.at(i).timestamp-prop_data.at(0).timestamp,imu_data.at(i).timestamp-time0);
            }
            // If the added IMU message doesn't end exactly at the camera time
            // Then we need to add another one that is right at the ending time
            if(prop_data.at(prop_data.size()-1).timestamp != time1) {
                IMUDATA data = interpolate_data(imu_data.at(i), imu_data.at(i+1), time1);
                prop_data.push_back(data);
                //printf("propagation #%d = CASE 3.3 = %.3f => %.3f\n", (int)i,data.timestamp-prop_data.at(0).timestamp,data.timestamp-time0);
            }
            break;
        }

    }

    // Check that we have at least one measurement to propagate with
    if(prop_data.empty()) {
        printf(YELLOW "Propagator::select_imu_readings(): No IMU measurements to propagate with (%d of 2). IMU-CAMERA are likely messed up!!!\n" RESET, (int)prop_data.size());
        return prop_data;
    }

    // If we did not reach the whole integration period (i.e., the last inertial measurement we have is smaller then the time we want to reach)
    // Then we should just "stretch" the last measurement to be the whole period (case 3 in the above loop)
    //if(time1-imu_data.at(imu_data.size()-1).timestamp > 1e-3) {
    //    printf(YELLOW "Propagator::select_imu_readings(): Missing inertial measurements to propagate with (%.6f sec missing). IMU-CAMERA are likely messed up!!!\n" RESET, (time1-imu_data.at(imu_data.size()-1).timestamp));
    //    return prop_data;
    //}

    // Loop through and ensure we do not have an zero dt values
    // This would cause the noise covariance to be Infinity
    for (size_t i=0; i < prop_data.size()-1; i++) {
        if (std::abs(prop_data.at(i+1).timestamp-prop_data.at(i).timestamp) < 1e-12) {
            printf(YELLOW "Propagator::select_imu_readings(): Zero DT between IMU reading %d and %d, removing it!\n" RESET, (int)i, (int)(i+1));
            prop_data.erase(prop_data.begin()+i);
            i--;
        }
    }

    // Check that we have at least one measurement to propagate with
    if(prop_data.size() < 2) {
        printf(YELLOW "Propagator::select_imu_readings(): No IMU measurements to propagate with (%d of 2). IMU-CAMERA are likely messed up!!!\n" RESET, (int)prop_data.size());
        return prop_data;
    }

    // Success :D
    return prop_data;

}

 

// Our vector imu readings

std::vector<Propagator::IMUDATA> prop_data;

선언

 

// Ensure we have some measurements in the first place!

if(imu_data.empty()) {

printf(YELLOW "Propagator::select_imu_readings(): No IMU measurements. IMU-CAMERA are likely messed up!!!\n" RESET);

return prop_data;

}

데이터 체크

 

// Loop through and find all the needed measurements to propagate with

// Note we split measurements based on the given state time, and the update timestamp

for(size_t i=0; i<imu_data.size()-1; i++) {

// START OF THE INTEGRATION PERIOD

// If the next timestamp is greater then our current state time

// And the current is not greater then it yet...

// Then we should "split" our current IMU measurement

if(imu_data.at(i+1).timestamp > time0 && imu_data.at(i).timestamp < time0) {

IMUDATA data = Propagator::interpolate_data(imu_data.at(i),imu_data.at(i+1), time0);

prop_data.push_back(data);

//printf("propagation #%d = CASE 1 = %.3f => %.3f\n", (int)i,data.timestamp-prop_data.at(0).timestamp,time0-prop_data.at(0).timestamp);

continue;

}

먼저 current state time이 두 개의 imu data timestamp 의 사이에 있는지 판단한다. 

만약 사이에 존재한다면, interpolate_data 함수를 사용하여 두 데이터 사이의 보간된 데이터 값을 얻어낸다.

그리고 이를 prop_data에 넣어준다. 

 

 

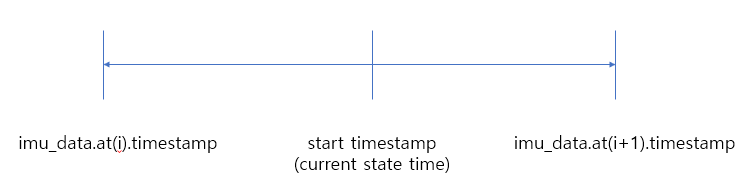
// MIDDLE OF INTEGRATION PERIOD

// If our imu measurement is right in the middle of our propagation period

// Then we should just append the whole measurement time to our propagation vector

if(imu_data.at(i).timestamp >= time0 && imu_data.at(i+1).timestamp <= time1) {

prop_data.push_back(imu_data.at(i));

//printf("propagation #%d = CASE 2 = %.3f\n",(int)i,imu_data.at(i).timestamp-prop_data.at(0).timestamp);

continue;

}

imu_data.at(i).timestamp >= time0 는 time0 가 begining imu data timestamp 보다 작다는 의미이며, 

imu_data.at(i+1).timestamp <= time1은 time1 이 end imu data timestamp 보다 크다는 의미이다.

즉, 두 imu data의 timestamp가 interval 사이에 존재한다면 imu_data.at(i)를 prop_data에 넣어주게 되는 것이다.

 

즉, time0와 time1 사이의 interval에는 항상 2개 이상의 데이터가 존재해야 하는데, 만약 "START OF THE INTEGRATION PERIOD"와 같이 interval의 시작이 될 시간보다 앞쪽에 imu_data.at(i)가 존재한다면 start imestamp를 하나의 imu_data로 만들어줌으로써, interval 간에는 "항상" imu_data가 존재하도록 만들어주는 것이다.

 

// END OF THE INTEGRATION PERIOD

// If the current timestamp is greater then our update time

// We should just "split" the NEXT IMU measurement to the update time,

// NOTE: we add the current time, and then the time at the end of the interval (so we can get a dt)

// NOTE: we also break out of this loop, as this is the last IMU measurement we need!

if(imu_data.at(i+1).timestamp > time1) {

// If we have a very low frequency IMU then, we could have only recorded the first integration (i.e. case 1) and nothing else

// In this case, both the current IMU measurement and the next is greater than the desired intepolation, thus we should just cut the current at the desired time

// Else, we have hit CASE2 and this IMU measurement is not past the desired propagation time, thus add the whole IMU reading

if(imu_data.at(i).timestamp > time1) {

IMUDATA data = interpolate_data(imu_data.at(i-1), imu_data.at(i), time1);

prop_data.push_back(data);

//printf("propagation #%d = CASE 3.1 = %.3f => %.3f\n", (int)i,imu_data.at(i).timestamp-prop_data.at(0).timestamp,imu_data.at(i).timestamp-time0);

} else {

prop_data.push_back(imu_data.at(i));

//printf("propagation #%d = CASE 3.2 = %.3f => %.3f\n", (int)i,imu_data.at(i).timestamp-prop_data.at(0).timestamp,imu_data.at(i).timestamp-time0);

}

// If the added IMU message doesn't end exactly at the camera time

// Then we need to add another one that is right at the ending time

if(prop_data.at(prop_data.size()-1).timestamp != time1) {

IMUDATA data = interpolate_data(imu_data.at(i), imu_data.at(i+1), time1);

prop_data.push_back(data);

//printf("propagation #%d = CASE 3.3 = %.3f => %.3f\n", (int)i,data.timestamp-prop_data.at(0).timestamp,data.timestamp-time0);

}

break;

}

 

여기서는 다음과 같은 경우를 보고있다.

imu data의 속도가 너무 느려서 interval 안에 아무 값도 존재하지 않는 것이다.

 

이런 경우엔 다음과 같이 (i-1)과 (i)의 interpolation을 수행하여 새로운 imu 값으로 사용해준다.

 

만약 마지막 imu data timestamp와 time interval의 time1 값이 일치하지 않는다면 아래와 같이 새로운 imu data를 보간하여 마지막 값으로 사용해준다.

 

// Check that we have at least one measurement to propagate with

if(prop_data.empty()) {

printf(YELLOW "Propagator::select_imu_readings(): No IMU measurements to propagate with (%d of 2). IMU-CAMERA are likely messed up!!!\n" RESET, (int)prop_data.size());

return prop_data;

}

 

propa_data 체크

 

// Loop through and ensure we do not have an zero dt values

// This would cause the noise covariance to be Infinity

for (size_t i=0; i < prop_data.size()-1; i++) {

if (std::abs(prop_data.at(i+1).timestamp-prop_data.at(i).timestamp) < 1e-12) {

printf(YELLOW "Propagator::select_imu_readings(): Zero DT between IMU reading %d and %d, removing it!\n" RESET, (int)i, (int)(i+1));

prop_data.erase(prop_data.begin()+i);

i--;

}

}

propa_data에 dt가 zero가 되게 만드는 요소가 있는지 확인하고, 있다면 지워버린다.

 

// Check that we have at least one measurement to propagate with

if(prop_data.size() < 2) {

printf(YELLOW "Propagator::select_imu_readings(): No IMU measurements to propagate with (%d of 2). IMU-CAMERA are likely messed up!!!\n" RESET, (int)prop_data.size());

return prop_data;

}

prop_data 데이터가 한개라도 있는지 확인한다.

 

// Success :D

return prop_data;

성공했다면 prop_data 벡터를 리턴한다.

 

 

 

 

 

 

 

Propagator::interpolate_data()

imu 센서의 rate가 빠르지 않아서 imu_1 과 imu_2 사이의 imu 값이 존재하지 않는 경우, 해당 시간을 이용한 보간법을 통해서 임의의 imu data 값을 구할 수 있다. 큰 그림은 다음과 같다. 즉, imu_1 이나 imu_2 중 더 가까운 값에 많은 비중을 둬서 값을 구하는 것이다.

        /**
         * @brief Nice helper function that will linearly interpolate between two imu messages.
         *
         * This should be used instead of just "cutting" imu messages that bound the camera times
         * Give better time offset if we use this function, could try other orders/splines if the imu is slow.
         *
         * @param imu_1 imu at begining of interpolation interval
         * @param imu_2 imu at end of interpolation interval
         * @param timestamp Timestamp being interpolated to
         */
        static IMUDATA interpolate_data(const IMUDATA imu_1, const IMUDATA imu_2, double timestamp) {
            // time-distance lambda
            double lambda = (timestamp - imu_1.timestamp) / (imu_2.timestamp - imu_1.timestamp);
            //cout << "lambda - " << lambda << endl;
            // interpolate between the two times
            IMUDATA data;
            data.timestamp = timestamp;
            data.am = (1 - lambda) * imu_1.am + lambda * imu_2.am;
            data.wm = (1 - lambda) * imu_1.wm + lambda * imu_2.wm;
            return data;
        }

 

predict_mean_rk4()

RK4는 룽게-쿠타(Runge-Kutta) 방법으로 적분 방정식 중 초기값 문제를 푸는 방법 중 하나이다.

참고하기 좋은 링크는 다음과 같다.

룽게-쿠타 방법

미분방정식에 대한 수치해석학적 해(Runge-Kutta) - 원리

[예제 4] Tunge-Kutta method for ODE

 

간단하게 설명하자면

다음과 같이 정의된 초기값 문제가 존재할 때,

( y의 미분이 f(t,y)라는 시간 t에대한 y 함수, 초깃값 y(t0) = y0)

위 문제를 해결하기 위한 다양한 접근법이 있는데,

룽게-쿠타 방법을 이용하면 다음을 구할 수 있게 된다.

즉 초기값 y(n)을 알고있고 y(n) 부터 y(n+1) 간의 시간(h)을 알고 있을 때,

이 시간 구간을 4구간으로 나누어서 각각에 대한 적분값을 구해 y(n+1)을 구하는 것이다.

이 때, k1, k2, k3, k4 는 다음과 같다.

 

아래 두 수식은 같은 내용이지만, 밑의 수식이 delta_t를 곱한다는 의미를 함께 담고있어서 가져왔다.

즉, t에 대해서 delta t만큼 한 칸씩 전진하면서 u(t_i) 값들을 추측해 나가는 것이다.

 

k1은 구간의 시작부분의 기울기에 의한 증분값을 의미하며,

k2는 구간의 중간의 기울기에 대한 증분값을,

k3도 구간의 중간의 기울기에 의한 증분값을,

k4는 구간의 끝의 기울기에 의한 증분값을 의미한다.

참고한 링크에 더 자세하게 설명이 되어있다. 

 

이 함수에서 우리가 구하려는 y는 다음과 같다.

1. imu의 회전 (quaternion)

2. imu의 pose

3. imu의 이동 (velocity)

 

        /**
         * @brief RK4 imu mean propagation.
         *
         * See this wikipedia page on [Runge-Kutta Methods](https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods).
         * We are doing a RK4 method, [this wolframe page](http://mathworld.wolfram.com/Runge-KuttaMethod.html) has the forth order equation defined below.
         * We define function \f$ f(t,y) \f$ where y is a function of time t, see @ref imu_kinematic for the definition of the continous-time functions.
         *
         * \f{align*}{
         * {k_1} &= f({t_0}, y_0) \Delta t  \\
         * {k_2} &= f( {t_0}+{\Delta t \over 2}, y_0 + {1 \over 2}{k_1} ) \Delta t \\
         * {k_3} &= f( {t_0}+{\Delta t \over 2}, y_0 + {1 \over 2}{k_2} ) \Delta t \\
         * {k_4} &= f( {t_0} + {\Delta t}, y_0 + {k_3} ) \Delta t \\
         * y_{0+\Delta t} &= y_0 + \left( {{1 \over 6}{k_1} + {1 \over 3}{k_2} + {1 \over 3}{k_3} + {1 \over 6}{k_4}} \right)
         * \f}
         *
         * @param state Pointer to state
         * @param dt Time we should integrate over
         * @param w_hat1 Angular velocity with bias removed
         * @param a_hat1 Linear acceleration with bias removed
         * @param w_hat2 Next angular velocity with bias removed
         * @param a_hat2 Next linear acceleration with bias removed
         * @param new_q The resulting new orientation after integration
         * @param new_v The resulting new velocity after integration
         * @param new_p The resulting new position after integration
         */
        void predict_mean_rk4(State *state, double dt,
                              const Eigen::Vector3d &w_hat1, const Eigen::Vector3d &a_hat1,
                              const Eigen::Vector3d &w_hat2, const Eigen::Vector3d &a_hat2,
                              Eigen::Vector4d &new_q, Eigen::Vector3d &new_v, Eigen::Vector3d &new_p);
                              
        void Propagator::predict_mean_rk4(State *state, double dt,
                                  const Eigen::Vector3d &w_hat1, const Eigen::Vector3d &a_hat1,
                                  const Eigen::Vector3d &w_hat2, const Eigen::Vector3d &a_hat2,
                                  Eigen::Vector4d &new_q, Eigen::Vector3d &new_v, Eigen::Vector3d &new_p) {

    // Pre-compute things
    Eigen::Vector3d w_hat = w_hat1;
    Eigen::Vector3d a_hat = a_hat1;
    Eigen::Vector3d w_alpha = (w_hat2-w_hat1)/dt;
    Eigen::Vector3d a_jerk = (a_hat2-a_hat1)/dt;

    // y0 ================
    Eigen::Vector4d q_0 = state->_imu->quat();
    Eigen::Vector3d p_0 = state->_imu->pos();
    Eigen::Vector3d v_0 = state->_imu->vel();

    // k1 ================
    Eigen::Vector4d dq_0 = {0,0,0,1};
    Eigen::Vector4d q0_dot = 0.5*Omega(w_hat)*dq_0;
    Eigen::Vector3d p0_dot = v_0;
    Eigen::Matrix3d R_Gto0 = quat_2_Rot(quat_multiply(dq_0,q_0));
    Eigen::Vector3d v0_dot = R_Gto0.transpose()*a_hat-_gravity;

    Eigen::Vector4d k1_q = q0_dot*dt;
    Eigen::Vector3d k1_p = p0_dot*dt;
    Eigen::Vector3d k1_v = v0_dot*dt;

    // k2 ================
    w_hat += 0.5*w_alpha*dt;
    a_hat += 0.5*a_jerk*dt;

    Eigen::Vector4d dq_1 = quatnorm(dq_0+0.5*k1_q);
    //Eigen::Vector3d p_1 = p_0+0.5*k1_p;
    Eigen::Vector3d v_1 = v_0+0.5*k1_v;

    Eigen::Vector4d q1_dot = 0.5*Omega(w_hat)*dq_1;
    Eigen::Vector3d p1_dot = v_1;
    Eigen::Matrix3d R_Gto1 = quat_2_Rot(quat_multiply(dq_1,q_0));
    Eigen::Vector3d v1_dot = R_Gto1.transpose()*a_hat-_gravity;

    Eigen::Vector4d k2_q = q1_dot*dt;
    Eigen::Vector3d k2_p = p1_dot*dt;
    Eigen::Vector3d k2_v = v1_dot*dt;

    // k3 ================
    Eigen::Vector4d dq_2 = quatnorm(dq_0+0.5*k2_q);
    //Eigen::Vector3d p_2 = p_0+0.5*k2_p;
    Eigen::Vector3d v_2 = v_0+0.5*k2_v;

    Eigen::Vector4d q2_dot = 0.5*Omega(w_hat)*dq_2;
    Eigen::Vector3d p2_dot = v_2;
    Eigen::Matrix3d R_Gto2 = quat_2_Rot(quat_multiply(dq_2,q_0));
    Eigen::Vector3d v2_dot = R_Gto2.transpose()*a_hat-_gravity;

    Eigen::Vector4d k3_q = q2_dot*dt;
    Eigen::Vector3d k3_p = p2_dot*dt;
    Eigen::Vector3d k3_v = v2_dot*dt;

    // k4 ================
    w_hat += 0.5*w_alpha*dt;
    a_hat += 0.5*a_jerk*dt;

    Eigen::Vector4d dq_3 = quatnorm(dq_0+k3_q);
    //Eigen::Vector3d p_3 = p_0+k3_p;
    Eigen::Vector3d v_3 = v_0+k3_v;

    Eigen::Vector4d q3_dot = 0.5*Omega(w_hat)*dq_3;
    Eigen::Vector3d p3_dot = v_3;
    Eigen::Matrix3d R_Gto3 = quat_2_Rot(quat_multiply(dq_3,q_0));
    Eigen::Vector3d v3_dot = R_Gto3.transpose()*a_hat-_gravity;

    Eigen::Vector4d k4_q = q3_dot*dt;
    Eigen::Vector3d k4_p = p3_dot*dt;
    Eigen::Vector3d k4_v = v3_dot*dt;

    // y+dt ================
    Eigen::Vector4d dq = quatnorm(dq_0+(1.0/6.0)*k1_q+(1.0/3.0)*k2_q+(1.0/3.0)*k3_q+(1.0/6.0)*k4_q);
    new_q = quat_multiply(dq, q_0);
    new_p = p_0+(1.0/6.0)*k1_p+(1.0/3.0)*k2_p+(1.0/3.0)*k3_p+(1.0/6.0)*k4_p;
    new_v = v_0+(1.0/6.0)*k1_v+(1.0/3.0)*k2_v+(1.0/3.0)*k3_v+(1.0/6.0)*k4_v;

}

// Pre-compute things

Eigen::Vector3d w_hat = w_hat1;

Eigen::Vector3d a_hat = a_hat1;

Eigen::Vector3d w_alpha = (w_hat2-w_hat1)/dt;

Eigen::Vector3d a_jerk = (a_hat2-a_hat1)/dt;

먼저 계산에 쓰일 값들을 구해준다.

w_hat은 회전에 대한 벡터이다. 수식은 w(t) 가 된다.

a_hat은 가속도에 대한 벡터이다. 수식은 a(t) 가 된다.

w_alpha는 회전에 대한 벡터를 t에 대해 미분한 값이다.

a_jerk는 가속도에 대한 벡터를 t에 대해 미분한 값이다.

 

// y0 ================

Eigen::Vector4d q_0 = state->_imu->quat();

Eigen::Vector3d p_0 = state->_imu->pos();

Eigen::Vector3d v_0 = state->_imu->vel();

먼저 초기값들을 구해준다. 

각각 아래와 같다.

1. imu의 회전 (quaternion)

2. imu의 pose

3. imu의 이동 (velocity)

 

즉 아래 수식 중 y(t0) = y0 가 생성된 것이다.

 

// k1 ================

Eigen::Vector4d dq_0 = {0,0,0,1};

Eigen::Vector4d q0_dot = 0.5*Omega(w_hat)*dq_0;

Eigen::Vector3d p0_dot = v_0;

Eigen::Matrix3d R_Gto0 = quat_2_Rot(quat_multiply(dq_0,q_0));

Eigen::Vector3d v0_dot = R_Gto0.transpose()*a_hat-_gravity;

Eigen::Vector4d k1_q = q0_dot*dt;

Eigen::Vector3d k1_p = p0_dot*dt;

Eigen::Vector3d k1_v = v0_dot*dt;

이제 아래 수식의 값을 구해야 한다.

그렇다면 저 f(tn,yn) 은 무엇인가?

해당 부분은 openvins의 documents에 잘 나와있다.

보면 알겠지만 q0_dot(quaternion)의 경우 0.5 와 w(t)에 대한 오메가 행렬 그리고 마지막 dq_0 를 곱하게 되는데 dq_0 부분은 확실치 않아서 차후에 reference(15)를 참고해야겠다.

20200709 내용 확인

 

Ground frame G 에서 Local frame L의 quaternion에 대한 미분은 다음과 같이 표현될 수 있다.

 

그리고 G에서 L(t+^t)의 quaternion은 다음과 같이 표현될 수 있다.

reference의 (69)를 참고하면 짧은 회전에 대한 quaternion은 다음과 같이 표현된다.

 그림으로 표현하면 다음과 같다.

 sin과 cos을 없애기 위해 first-order taylor expansion을 적용하면 다음과 같다.

 위의 공식을 이용하면 다음과 같이 변환된다.

이 때, k_hat은 vector의 회전 방향과 회전 크기에 대한 벡터이며, 이를 가장 오른쪽 항의 delta-theta로 바꿀 수 있다.

이 delta-theta를 시간에 대해 미분하면 회전 속도(w)이 된다.

 

 이를 이용하면 다음과 같은 전개가 가능하다.

 p0_dot과 v0_dot은 어렵지 않다.

p0_dot(pose)는 velocity 값을 이용하게 된다. (위치의 미분은 속도)

마지막으로 v0_dot(velocity)는 회전행렬과 가속도를 곱하게 된다. (속도의 미분은 가속도)

 

자, 이렇게 우리는 q0_dot과 p0_dot과 v0_dot의 미분값을 구했다.

이제 k1 값을 구하면 된다.

 

 그러므로 각각의 결과에 dt를 곱하여 최종적으로 k1_q,  k1_p, k1_v를 구하게 된다.

 

// k2 ================

w_hat += 0.5*w_alpha*dt;

a_hat += 0.5*a_jerk*dt;

Eigen::Vector4d dq_1 = quatnorm(dq_0+0.5*k1_q);

//Eigen::Vector3d p_1 = p_0+0.5*k1_p;

Eigen::Vector3d v_1 = v_0+0.5*k1_v;

Eigen::Vector4d q1_dot = 0.5*Omega(w_hat)*dq_1;

Eigen::Vector3d p1_dot = v_1;

Eigen::Matrix3d R_Gto1 = quat_2_Rot(quat_multiply(dq_1,q_0));

Eigen::Vector3d v1_dot = R_Gto1.transpose()*a_hat-_gravity;

Eigen::Vector4d k2_q = q1_dot*dt;

Eigen::Vector3d k2_p = p1_dot*dt;

Eigen::Vector3d k2_v = v1_dot*dt;

이제 아래 내용을 진행한다.

차후에 더 자세히 적어보겠다.

 

20200709 내용 정리

 

 위 수식에 해당하는 ui+1/2*k1 을 만들어준 뒤,

해당 kinematics에 맞게 각 값들을 다시 만들어주고

dt를 곱하여 k2_q, k2_p, k2_v를 구하게 된다.

 

 

// k3 ================

Eigen::Vector4d dq_2 = quatnorm(dq_0+0.5*k2_q);

//Eigen::Vector3d p_2 = p_0+0.5*k2_p;

Eigen::Vector3d v_2 = v_0+0.5*k2_v;

Eigen::Vector4d q2_dot = 0.5*Omega(w_hat)*dq_2;

Eigen::Vector3d p2_dot = v_2;

Eigen::Matrix3d R_Gto2 = quat_2_Rot(quat_multiply(dq_2,q_0));

Eigen::Vector3d v2_dot = R_Gto2.transpose()*a_hat-_gravity;

Eigen::Vector4d k3_q = q2_dot*dt;

Eigen::Vector3d k3_p = p2_dot*dt;

Eigen::Vector3d k3_v = v2_dot*dt;

이제 아래 내용을 진행한다.

차후에 더 자세히 진행하겠다.

 

20200709 내용 확인

 위 내용을 이용하여 앞의 k2 구하기와 똑같은 과정으로 진행된다.

 

 

 

 

 

 

// k4 ================

w_hat += 0.5*w_alpha*dt;

a_hat += 0.5*a_jerk*dt;

Eigen::Vector4d dq_3 = quatnorm(dq_0+k3_q);

//Eigen::Vector3d p_3 = p_0+k3_p;

Eigen::Vector3d v_3 = v_0+k3_v;

Eigen::Vector4d q3_dot = 0.5*Omega(w_hat)*dq_3;

Eigen::Vector3d p3_dot = v_3;

Eigen::Matrix3d R_Gto3 = quat_2_Rot(quat_multiply(dq_3,q_0));

Eigen::Vector3d v3_dot = R_Gto3.transpose()*a_hat-_gravity;

Eigen::Vector4d k4_q = q3_dot*dt;

Eigen::Vector3d k4_p = p3_dot*dt;

Eigen::Vector3d k4_v = v3_dot*dt;

이제 아래 내용을 진행한다.

차후에 더 자세히 진행하겠다.

 

20200709 내용 정리

 

 이제 위 내용을 진행하여 k4_q, k4_p, k4_v 를 진행한다.

 

 

 

 

 

 

// y+dt ================

Eigen::Vector4d dq = quatnorm(dq_0+(1.0/6.0)*k1_q+(1.0/3.0)*k2_q+(1.0/3.0)*k3_q+(1.0/6.0)*k4_q);

new_q = quat_multiply(dq, q_0);

new_p = p_0+(1.0/6.0)*k1_p+(1.0/3.0)*k2_p+(1.0/3.0)*k3_p+(1.0/6.0)*k4_p;

new_v = v_0+(1.0/6.0)*k1_v+(1.0/3.0)*k2_v+(1.0/3.0)*k3_v+(1.0/6.0)*k4_v;

마지막으로 다음 내용을 진행한다.

이렇게 y(n+1)을 구하게 된다.

20200709 내용 정리

 

 이제 위의 수식을 구하게 되는데, 이 때, quaternion은 이전 값에 바로 더할 수 없으므로 quat_multiply를 사용해준다.

이렇게 최종적으로 new_q, new_p, new_v를 구하게 된다.

predict_and_compute()

우리는 최종적으로 다음의 수식을 구하고자 한다.

해당 함수에서는 위 수식에 사용되는 다음의 행렬들을 구하게 된다.

System Jacobian Matrix

Noise Jaconian Matrix

continuous-time measurement noises

descrete-time noise covariance

이 때, System Jacobian Matrix는 code에서 "F"로 나타내며, 다음과 같은 행렬이 된다. 

각 요소는 3x3 행렬이므로, 총 행렬 크기는 15x15가 된다.

System Jacobian Matrix

그리고 Noise Jacobian Matrix는 code에서 "G"로 나타내며, 다음과 같은 행렬이 된다.

각 요소는 3x3 행렬이므로, 총 행렬 크기는 15x15가 된다.

Noise Jacobian Matrix

Qc와 Qd는 Indirect Kalman Filter for 3D Attitude Estimation를 참고하면 다음과 같은 형태이다.

continuous-time measurement noises

discrete-time noise covariance

 

        /**
         * @brief Propagates the state forward using the imu data and computes the noise covariance and state-transition
         * matrix of this interval.
         *
         * This function can be replaced with analytical/numerical integration or when using a different state representation.
         * This contains our state transition matrix along with how our noise evolves in time.
         * If you have other state variables besides the IMU that evolve you would add them here.
         * See the @ref error_prop page for details on how this was derived.
         *
         * @param state Pointer to state
         * @param data_minus imu readings at beginning of interval
         * @param data_plus imu readings at end of interval
         * @param F State-transition matrix over the interval
         * @param Qd Discrete-time noise covariance over the interval
         */
        void predict_and_compute(State *state, const IMUDATA data_minus, const IMUDATA data_plus,
                                 Eigen::Matrix<double, 15, 15> &F, Eigen::Matrix<double, 15, 15> &Qd);


void Propagator::predict_and_compute(State *state, const IMUDATA data_minus, const IMUDATA data_plus,
                                     Eigen::Matrix<double,15,15> &F, Eigen::Matrix<double,15,15> &Qd) {

    // Set them to zero
    F.setZero();
    Qd.setZero();

    // Time elapsed over interval
    double dt = data_plus.timestamp-data_minus.timestamp;
    //assert(data_plus.timestamp>data_minus.timestamp);

    // Corrected imu measurements
    Eigen::Matrix<double,3,1> w_hat = data_minus.wm - state->_imu->bias_g();
    Eigen::Matrix<double,3,1> a_hat = data_minus.am - state->_imu->bias_a();
    Eigen::Matrix<double,3,1> w_hat2 = data_plus.wm - state->_imu->bias_g();
    Eigen::Matrix<double,3,1> a_hat2 = data_plus.am - state->_imu->bias_a();

    // Compute the new state mean value
    Eigen::Vector4d new_q;
    Eigen::Vector3d new_v, new_p;
    if(state->_options.use_rk4_integration) predict_mean_rk4(state, dt, w_hat, a_hat, w_hat2, a_hat2, new_q, new_v, new_p);
    else predict_mean_discrete(state, dt, w_hat, a_hat, w_hat2, a_hat2, new_q, new_v, new_p);

    // Get the locations of each entry of the imu state
    int th_id = state->_imu->q()->id()-state->_imu->id();
    int p_id = state->_imu->p()->id()-state->_imu->id();
    int v_id = state->_imu->v()->id()-state->_imu->id();
    int bg_id = state->_imu->bg()->id()-state->_imu->id();
    int ba_id = state->_imu->ba()->id()-state->_imu->id();

    // Allocate noise Jacobian
    Eigen::Matrix<double,15,12> G = Eigen::Matrix<double,15,12>::Zero();

    // Now compute Jacobian of new state wrt old state and noise
    if (state->_options.do_fej) {

        // This is the change in the orientation from the end of the last prop to the current prop
        // This is needed since we need to include the "k-th" updated orientation information
        Eigen::Matrix<double,3,3> Rfej = state->_imu->Rot_fej();
        Eigen::Matrix<double,3,3> dR = quat_2_Rot(new_q)*Rfej.transpose();

        Eigen::Matrix<double,3,1> v_fej = state->_imu->vel_fej();
        Eigen::Matrix<double,3,1> p_fej = state->_imu->pos_fej();

        F.block(th_id, th_id, 3, 3) = dR;
        F.block(th_id, bg_id, 3, 3).noalias() = -dR * Jr_so3(-w_hat * dt) * dt;
        //F.block(th_id, bg_id, 3, 3).noalias() = -dR * Jr_so3(-log_so3(dR)) * dt;
        F.block(bg_id, bg_id, 3, 3).setIdentity();
        F.block(v_id, th_id, 3, 3).noalias() = -skew_x(new_v-v_fej+_gravity*dt)*Rfej.transpose();
        //F.block(v_id, th_id, 3, 3).noalias() = -Rfej.transpose() * skew_x(Rfej*(new_v-v_fej+_gravity*dt));
        F.block(v_id, v_id, 3, 3).setIdentity();
        F.block(v_id, ba_id, 3, 3) = -Rfej.transpose() * dt;
        F.block(ba_id, ba_id, 3, 3).setIdentity();
        F.block(p_id, th_id, 3, 3).noalias() = -skew_x(new_p-p_fej-v_fej*dt+0.5*_gravity*dt*dt)*Rfej.transpose();
        //F.block(p_id, th_id, 3, 3).noalias() = -0.5 * Rfej.transpose() * skew_x(2*Rfej*(new_p-p_fej-v_fej*dt+0.5*_gravity*dt*dt));
        F.block(p_id, v_id, 3, 3) = Eigen::Matrix<double, 3, 3>::Identity() * dt;
        F.block(p_id, ba_id, 3, 3) = -0.5 * Rfej.transpose() * dt * dt;
        F.block(p_id, p_id, 3, 3).setIdentity();

        G.block(th_id, 0, 3, 3) = -dR * Jr_so3(-w_hat * dt) * dt;
        //G.block(th_id, 0, 3, 3) = -dR * Jr_so3(-log_so3(dR)) * dt;
        G.block(v_id, 3, 3, 3) = -Rfej.transpose() * dt;
        G.block(p_id, 3, 3, 3) = -0.5 * Rfej.transpose() * dt * dt;
        G.block(bg_id, 6, 3, 3) = dt*Eigen::Matrix<double,3,3>::Identity();
        G.block(ba_id, 9, 3, 3) = dt*Eigen::Matrix<double,3,3>::Identity();

    } else {

        Eigen::Matrix<double,3,3> R_Gtoi = state->_imu->Rot();

        F.block(th_id, th_id, 3, 3) = exp_so3(-w_hat * dt);
        F.block(th_id, bg_id, 3, 3).noalias() = -exp_so3(-w_hat * dt) * Jr_so3(-w_hat * dt) * dt;
        F.block(bg_id, bg_id, 3, 3).setIdentity();
        F.block(v_id, th_id, 3, 3).noalias() = -R_Gtoi.transpose() * skew_x(a_hat * dt);
        F.block(v_id, v_id, 3, 3).setIdentity();
        F.block(v_id, ba_id, 3, 3) = -R_Gtoi.transpose() * dt;
        F.block(ba_id, ba_id, 3, 3).setIdentity();
        F.block(p_id, th_id, 3, 3).noalias() = -0.5 * R_Gtoi.transpose() * skew_x(a_hat * dt * dt);
        F.block(p_id, v_id, 3, 3) = Eigen::Matrix<double, 3, 3>::Identity() * dt;
        F.block(p_id, ba_id, 3, 3) = -0.5 * R_Gtoi.transpose() * dt * dt;
        F.block(p_id, p_id, 3, 3).setIdentity();

        G.block(th_id, 0, 3, 3) = -exp_so3(-w_hat * dt) * Jr_so3(-w_hat * dt) * dt;
        G.block(v_id, 3, 3, 3) = -R_Gtoi.transpose() * dt;
        G.block(p_id, 3, 3, 3) = -0.5 * R_Gtoi.transpose() * dt * dt;
        G.block(bg_id, 6, 3, 3) = dt*Eigen::Matrix<double,3,3>::Identity();
        G.block(ba_id, 9, 3, 3) = dt*Eigen::Matrix<double,3,3>::Identity();
    }

    // Construct our discrete noise covariance matrix
    // Note that we need to convert our continuous time noises to discrete
    // Equations (129) amd (130) of Trawny tech report
    Eigen::Matrix<double,12,12> Qc = Eigen::Matrix<double,12,12>::Zero();
    Qc.block(0,0,3,3) = _noises.sigma_w_2/dt*Eigen::Matrix<double,3,3>::Identity();
    Qc.block(3,3,3,3) = _noises.sigma_a_2/dt*Eigen::Matrix<double,3,3>::Identity();
    Qc.block(6,6,3,3) = _noises.sigma_wb_2/dt*Eigen::Matrix<double,3,3>::Identity();
    Qc.block(9,9,3,3) = _noises.sigma_ab_2/dt*Eigen::Matrix<double,3,3>::Identity();

    // Compute the noise injected into the state over the interval
    Qd = G*Qc*G.transpose();
    Qd = 0.5*(Qd+Qd.transpose());

    //Now replace imu estimate and fej with propagated values
    Eigen::Matrix<double,16,1> imu_x = state->_imu->value();
    imu_x.block(0,0,4,1) = new_q;
    imu_x.block(4,0,3,1) = new_p;
    imu_x.block(7,0,3,1) = new_v;
    state->_imu->set_value(imu_x);
    state->_imu->set_fej(imu_x);

}

// Set them to zero

F.setZero();

Qd.setZero();

먼저 행렬을 초기화 해준다.

 

// Time elapsed over interval

double dt = data_plus.timestamp-data_minus.timestamp;

//assert(data_plus.timestamp>data_minus.timestamp);

두 개 imu data 간의 시간 간격을 구한다.

 

// Corrected imu measurements

Eigen::Matrix<double,3,1> w_hat = data_minus.wm - state->_imu->bias_g();

Eigen::Matrix<double,3,1> a_hat = data_minus.am - state->_imu->bias_a();

Eigen::Matrix<double,3,1> w_hat2 = data_plus.wm - state->_imu->bias_g();

Eigen::Matrix<double,3,1> a_hat2 = data_plus.am - state->_imu->bias_a();

측정된 imu data에서 bias 값을 뺌으로써 real imu data 값을 추정해서 사용한다. 

이를 w_hat, a_hat 이라 한다.

 

// Compute the new state mean value

Eigen::Vector4d new_q;

Eigen::Vector3d new_v, new_p;

if(state->_options.use_rk4_integration) predict_mean_rk4(state, dt, w_hat, a_hat, w_hat2, a_hat2, new_q, new_v, new_p);

else predict_mean_discrete(state, dt, w_hat, a_hat, w_hat2, a_hat2, new_q, new_v, new_p);

우리 시스템에서는 predict_mean_rk4() 를 사용하며, 

y(n)으로부터 y(n+1)의 값을 추측하게 된다. 

그 결과가 new_q, new_v, new_p 가 된다.

 

// Get the locations of each entry of the imu state

int th_id = state->_imu->q()->id()-state->_imu->id();

int p_id = state->_imu->p()->id()-state->_imu->id();

int v_id = state->_imu->v()->id()-state->_imu->id();

int bg_id = state->_imu->bg()->id()-state->_imu->id();

int ba_id = state->_imu->ba()->id()-state->_imu->id();

imu 상태의 각 항목 ( q, p, v, bg, ba )의 id를 가져온다.

 

// Allocate noise Jacobian

Eigen::Matrix<double,15,12> G = Eigen::Matrix<double,15,12>::Zero();

noise Jacobian을 선언한다.

 

// Now compute Jacobian of new state wrt old state and noise

if (state->_options.do_fej) {

이제 old state와 noise와 관련한 새로운 상태의 Jacobian을 계산한다.

 

여기서 "do_fej" 옵션에 따라서 두가지 계산이 존재하게 되는데, 우리 시스템에서는 fej를 사용하니 해당 부분으로 연산을 진행하자.

 

// This is the change in the orientation from the end of the last prop to the current prop

// This is needed since we need to include the "k-th" updated orientation information

Eigen::Matrix<double,3,3> Rfej = state->_imu->Rot_fej();

Eigen::Matrix<double,3,3> dR = quat_2_Rot(new_q)*Rfej.transpose();

먼저 state->_imu->Rot_fej() 함수를 통해 imu의 회전 행렬을 가져온다.

이 후, new_q를 통해 얻어낸 새로운 회전 행렬과 이 전의 회전 행렬을 곱하여서

누적 계산된 회전 변화를 의미하게 되는 dR을 구하게 된다. 

 

Eigen::Matrix<double,3,1> v_fej = state->_imu->vel_fej();

Eigen::Matrix<double,3,1> p_fej = state->_imu->pos_fej();

다음으로 velocity와 pose를 가져온다.

 

F.block(th_id, th_id, 3, 3) = dR;

F.block(th_id, bg_id, 3, 3).noalias() = -dR * Jr_so3(-w_hat * dt) * dt;

//F.block(th_id, bg_id, 3, 3).noalias() = -dR * Jr_so3(-log_so3(dR)) * dt;

F.block(bg_id, bg_id, 3, 3).setIdentity();

F.block(v_id, th_id, 3, 3).noalias() = -skew_x(new_v-v_fej+_gravity*dt)*Rfej.transpose();

//F.block(v_id, th_id, 3, 3).noalias() = -Rfej.transpose() * skew_x(Rfej*(new_v-v_fej+_gravity*dt));

F.block(v_id, v_id, 3, 3).setIdentity();

F.block(v_id, ba_id, 3, 3) = -Rfej.transpose() * dt;

F.block(ba_id, ba_id, 3, 3).setIdentity();

F.block(p_id, th_id, 3, 3).noalias() = -skew_x(new_p-p_fej-v_fej*dt+0.5*_gravity*dt*dt)*Rfej.transpose();

//F.block(p_id, th_id, 3, 3).noalias() = -0.5 * Rfej.transpose() * skew_x(2*Rfej*(new_p-p_fej-v_fej*dt+0.5*_gravity*dt*dt));

F.block(p_id, v_id, 3, 3) = Eigen::Matrix<double, 3, 3>::Identity() * dt;

F.block(p_id, ba_id, 3, 3) = -0.5 * Rfej.transpose() * dt * dt;

F.block(p_id, p_id, 3, 3).setIdentity();

System Jacobian Matrix

이제 system jacobian matrix를 구해준다. 자세한 내용은 추후에 진행하도록 하자.

 

20200714 내용 진행

 

참고링크

state vector는 다음과 같이 구성된다.

 

state vector

 

그리고 discrete time error-state propagation 단계에서 error-state x는 다음과 같다.

 

error-state

 이 때, big-pie 는 transition matrix 이고, Gk는 noise jacobian matrix 이다.

 

이 때, xi 는 다음과 같다.

 

error-state vector

 

그리고 big-pie 에는 x state에서 발생한 변화에 대한 내용이 들어가게 된다.

1. rotation

2. position

3. velocity

에 대한 내용이 각각 들어가게 된다.

 

먼저 rotation은 다음과 같은 과정을 통해 구해진다.

 

 이 때, Jr은 다음을 참고한다.

ov_core::Jr_so3()

 

최종적으로 다음과 같은  rotation 식을 구하게 된다.

 

 position은 다음과 같은 과정을 통해 구해진다.

 

 

velocity는 다음과 같은 과정을 통해 구해진다.

 

 각 항에 곱해져 있는 변수들 중 state 안에 존재하는 값들이 있다.

theta와 (b+n)이라는 노이즈가 그것인데, 이를 이용해 다음과 같이 매칭된 위치에 인자를 넣게 된다.

 

 

 

 

 

G.block(th_id, 0, 3, 3) = -dR * Jr_so3(-w_hat * dt) * dt;

//G.block(th_id, 0, 3, 3) = -dR * Jr_so3(-log_so3(dR)) * dt;

G.block(v_id, 3, 3, 3) = -Rfej.transpose() * dt;

G.block(p_id, 3, 3, 3) = -0.5 * Rfej.transpose() * dt * dt;

G.block(bg_id, 6, 3, 3) = dt*Eigen::Matrix<double,3,3>::Identity();

G.block(ba_id, 9, 3, 3) = dt*Eigen::Matrix<double,3,3>::Identity();

Noise Jacobian Matrix

이제 noise jacobian matrix를 구해주도록 한다. 자세한 내용은 추후에 진행하도록 하자.

 

20200714 내용 정리

 

noise vector의 구조의 경우 다음과 같은 구조를 갖는다.

 

 우리는 이미 transition matrix를 구할 때 ng와 na에 대한 gaussian noise는 구하였다.

bias noise는 다음과 같이 구해지게 된다.

 

 

이를 이용해 noise jacobian를 구하면 다음과 같다.

 

 

 

 

// Construct our discrete noise covariance matrix

// Note that we need to convert our continuous time noises to discrete

// Equations (129) amd (130) of Trawny tech report

Eigen::Matrix<double,12,12> Qc = Eigen::Matrix<double,12,12>::Zero();

Qc.block(0,0,3,3) = _noises.sigma_w_2/dt*Eigen::Matrix<double,3,3>::Identity();

Qc.block(3,3,3,3) = _noises.sigma_a_2/dt*Eigen::Matrix<double,3,3>::Identity();

Qc.block(6,6,3,3) = _noises.sigma_wb_2/dt*Eigen::Matrix<double,3,3>::Identity();

Qc.block(9,9,3,3) = _noises.sigma_ab_2/dt*Eigen::Matrix<double,3,3>::Identity();

이제 Qc를 구해준다. 

먼저 시작하기 전에 gyro sensor의 noise model을 알아야 한다.

 아래와 같이 gyro의 측정 값 wm은 raw data w와 bias noise b와 rate noise nr로 구성되어 있다. 

 그리고 Gaussian white noise nr은 다음과 같은 특성을 갖고 있다고 하자.

 bias noise b의 random walk를 nw라 표현하자.

 그리고 이는 다음과 같은 특성을 갖고 있다고 하자.

 이 때, Nr과 Nw는 다음과 같다.

 이 때, c는 continuous-time을 의미한다.

 

아래와 같은 연산의 단위는 rad^2/sec^2 이다.

이 때, 걸린 시간을 미분단위로 쪼갠 sigma(tau)는 다음과 같기 때문에,

 low_rc^2의 단위는 다음과 같아진다.

회전 가속도를 의미하는 sigma_rc의 단위로 이해해도 된다. ( 회전 각의 제곱을 시간으로 나누면 가속도)

 random walk의 경우엔 다음과 같다.

discrete time 에서는 sigma_rd와 sigma_wd가 같은 turn rate를 갖고 있어야 한다.(rad/sec)

이를 위해 다음의 연산을 진행할 수 있다. 

 

 

 

Continous time error state 에서 noise covariance matrix Qc는 다음과 같다.

 

noise covatiance matrix

 지금까지 내용들을 이용해 계산을 진행해주면 다음과 같다.

_noises.sigma_w_2, _noises.sigma_a_2, _noises.sigma_bw_2, _noises.sigma_ba_2

위 변수들은 각각 w,a,bw,ba를 "제곱"한 값이다. 그리고 이를 dt로 나누었다는 것은 sigma_r(white gaussian noise)를 discrete time에 대해 구해주었다는 의미가 된다.

 

이는 이렇게 표현할 수도 있다.

 

 

 

 

// Compute the noise injected into the state over the interval

Qd = G*Qc*G.transpose();

Qd = 0.5*(Qd+Qd.transpose());

이제 Qc와 Qd를 계산한다. 이 또한 자세한 내용은 추후에 진행하자.

 

20200714 내용정리

Qd에 대체 왜 이런 연산을 한걸까?

 

 

 

//Now replace imu estimate and fej with propagated values

Eigen::Matrix<double,16,1> imu_x = state->_imu->value();

imu_x.block(0,0,4,1) = new_q;

imu_x.block(4,0,3,1) = new_p;

imu_x.block(7,0,3,1) = new_v;

state->_imu->set_value(imu_x);

state->_imu->set_fej(imu_x);

이제 원래 측정되었던 imu data 값을 새롭게 propagate한 imu value 값으로 replace 해준다.

 

StateHelper::EKFPropagation()

        /**
         * @brief Performs EKF propagation of the state covariance.
         *
         * The mean of the state should already have been propagated, thus just moves the covariance forward in time.
         * The new states that we are propagating the old covariance into, should be **contiguous** in memory.
         * The user only needs to specify the sub-variables that this block is a function of.
         * \f[
         * \tilde{\mathbf{x}}' =
         * \begin{bmatrix}
         * \boldsymbol\Phi_1 &
         * \boldsymbol\Phi_2 &
         * \boldsymbol\Phi_3
         * \end{bmatrix}
         * \begin{bmatrix}
         * \tilde{\mathbf{x}}_1 \\
         * \tilde{\mathbf{x}}_2 \\
         * \tilde{\mathbf{x}}_3
         * \end{bmatrix}
         * +
         * \mathbf{n}
         * \f]
         *
         * @param state Pointer to state
         * @param order_NEW Contiguous variables that have evolved according to this state transition
         * @param order_OLD Variable ordering used in the state transition
         * @param Phi State transition matrix (size order_NEW by size order_OLD)
         * @param Q Additive state propagation noise matrix (size order_NEW by size order_NEW)
         */
        static void EKFPropagation(State *state, const std::vector<Type*> &order_NEW, const std::vector<Type*> &order_OLD,
                                   const Eigen::MatrixXd &Phi, const Eigen::MatrixXd &Q);
                                   
                                   void StateHelper::EKFPropagation(State *state, const std::vector<Type*> &order_NEW, const std::vector<Type*> &order_OLD,
                                 const Eigen::MatrixXd &Phi, const Eigen::MatrixXd &Q) {

    // We need at least one old and new variable
    if (order_NEW.empty() || order_OLD.empty()) {
        printf(RED "StateHelper::EKFPropagation() - Called with empty variable arrays!\n" RESET);
        std::exit(EXIT_FAILURE);
    }

    // Loop through our Phi order and ensure that they are continuous in memory
    int size_order_NEW = order_NEW.at(0)->size();
    for(size_t i=0; i<order_NEW.size()-1; i++) {
        if(order_NEW.at(i)->id()+order_NEW.at(i)->size()!=order_NEW.at(i+1)->id()) {
            printf(RED "StateHelper::EKFPropagation() - Called with non-contiguous state elements!\n" RESET);
            printf(RED "StateHelper::EKFPropagation() - This code only support a state transition which is in the same order as the state\n" RESET);
            std::exit(EXIT_FAILURE);
        }
        size_order_NEW += order_NEW.at(i+1)->size();
    }

    // Size of the old phi matrix
    int size_order_OLD = order_OLD.at(0)->size();
    for(size_t i=0; i<order_OLD.size()-1; i++) {
        size_order_OLD += order_OLD.at(i+1)->size();
    }

    // Assert that we have correct sizes
    assert(size_order_NEW==Phi.rows());
    assert(size_order_OLD==Phi.cols());
    assert(size_order_NEW==Q.cols());
    assert(size_order_NEW==Q.rows());

    // Get the location in small phi for each measuring variable
    int current_it = 0;
    std::vector<int> Phi_id;
    for (Type *var: order_OLD) {
        Phi_id.push_back(current_it);
        current_it += var->size();
    }

    // Loop through all our old states and get the state transition times it
    // Cov_PhiT = [ Pxx ] [ Phi' ]'
    Eigen::MatrixXd Cov_PhiT = Eigen::MatrixXd::Zero(state->_Cov.rows(), Phi.rows());
    for (size_t i=0; i<order_OLD.size(); i++) {
        Type *var = order_OLD.at(i);
        Cov_PhiT.noalias() += state->_Cov.block(0, var->id(), state->_Cov.rows(), var->size())
                              * Phi.block(0, Phi_id[i], Phi.rows(), var->size()).transpose();

    }

    // Get Phi_NEW*Covariance*Phi_NEW^t + Q
    Eigen::MatrixXd Phi_Cov_PhiT = Q.selfadjointView<Eigen::Upper>();
    for (size_t i=0; i<order_OLD.size(); i++) {
        Type *var = order_OLD.at(i);
        Phi_Cov_PhiT.noalias() += Phi.block(0, Phi_id[i], Phi.rows(), var->size())
                                  * Cov_PhiT.block(var->id(), 0, var->size(), Phi.rows());
    }

    // We are good to go!
    int start_id = order_NEW.at(0)->id();
    int phi_size = Phi.rows();
    int total_size = state->_Cov.rows();
    state->_Cov.block(start_id,0,phi_size,total_size) = Cov_PhiT.transpose();
    state->_Cov.block(0,start_id,total_size,phi_size) = Cov_PhiT;
    state->_Cov.block(start_id,start_id,phi_size,phi_size) = Phi_Cov_PhiT;

    // We should check if we are not positive semi-definitate (i.e. negative diagionals is not s.p.d)
    Eigen::VectorXd diags = state->_Cov.diagonal();
    bool found_neg = false;
    for(int i=0; i<diags.rows(); i++) {
        if(diags(i) < 0.0) {
            printf(RED "StateHelper::EKFPropagation() - diagonal at %d is %.2f\n" RESET,i,diags(i));
            found_neg = true;
        }
    }
    assert(!found_neg);

}

// We need at least one old and new variable

if (order_NEW.empty() || order_OLD.empty()) {

printf(RED "StateHelper::EKFPropagation() - Called with empty variable arrays!\n" RESET);

std::exit(EXIT_FAILURE);

}

state 데이터 체크

 

// Loop through our Phi order and ensure that they are continuous in memory

int size_order_NEW = order_NEW.at(0)->size();

for(size_t i=0; i<order_NEW.size()-1; i++) {

if(order_NEW.at(i)->id()+order_NEW.at(i)->size()!=order_NEW.at(i+1)->id()) {

printf(RED "StateHelper::EKFPropagation() - Called with non-contiguous state elements!\n" RESET);

printf(RED "StateHelper::EKFPropagation() - This code only support a state transition which is in the same order as the state\n" RESET);

std::exit(EXIT_FAILURE);

}

size_order_NEW += order_NEW.at(i+1)->size();

}

state 데이터 체크

 

// Size of the old phi matrix

int size_order_OLD = order_OLD.at(0)->size();

for(size_t i=0; i<order_OLD.size()-1; i++) {

size_order_OLD += order_OLD.at(i+1)->size();

}

state 데이터 체크

 

// Assert that we have correct sizes

assert(size_order_NEW==Phi.rows());

assert(size_order_OLD==Phi.cols());

assert(size_order_NEW==Q.cols());

assert(size_order_NEW==Q.rows());

Phi, transition  matrix의 사이즈 체크

Q, state propagation noise matrix의 사이즈 체크

 

// Get the location in small phi for each measuring variable

int current_it = 0;

std::vector<int> Phi_id;

for (Type *var: order_OLD) {

Phi_id.push_back(current_it);

current_it += var->size();

}

  vector Phi_id를 만들어 Phi의 각 id를 Phi_id에 넣음.

 

// Loop through all our old states and get the state transition times it

// Cov_PhiT = [ Pxx ] [ Phi' ]'

Eigen::MatrixXd Cov_PhiT = Eigen::MatrixXd::Zero(state->_Cov.rows(), Phi.rows());

for (size_t i=0; i<order_OLD.size(); i++) {

Type *var = order_OLD.at(i);

Cov_PhiT.noalias() += state->_Cov.block(0, var->id(), state->_Cov.rows(), var->size())

* Phi.block(0, Phi_id[i], Phi.rows(), var->size()).transpose();

}

Covariance Matrix 와 Phi Matrix의 transpose를 곱한 Cov_PhiT Matrix를 만듦.

 

// Get Phi_NEW*Covariance*Phi_NEW^t + Q

Eigen::MatrixXd Phi_Cov_PhiT = Q.selfadjointView<Eigen::Upper>();

for (size_t i=0; i<order_OLD.size(); i++) {

Type *var = order_OLD.at(i);

Phi_Cov_PhiT.noalias() += Phi.block(0, Phi_id[i], Phi.rows(), var->size())

* Cov_PhiT.block(var->id(), 0, var->size(), Phi.rows());

}

Phi Matrix를 한번 더 곱해준 Phi_Cov_PhiT 를 구해준다.

 

// We are good to go!

int start_id = order_NEW.at(0)->id();

int phi_size = Phi.rows();

int total_size = state->_Cov.rows();

state->_Cov.block(start_id,0,phi_size,total_size) = Cov_PhiT.transpose();

state->_Cov.block(0,start_id,total_size,phi_size) = Cov_PhiT;

state->_Cov.block(start_id,start_id,phi_size,phi_size) = Phi_Cov_PhiT;

행렬들을 state->_Cov 에 저장한다.

 

// We should check if we are not positive semi-definitate (i.e. negative diagionals is not s.p.d)

Eigen::VectorXd diags = state->_Cov.diagonal();

bool found_neg = false;

for(int i=0; i<diags.rows(); i++) {

if(diags(i) < 0.0) {

printf(RED "StateHelper::EKFPropagation() - diagonal at %d is %.2f\n" RESET,i,diags(i));

found_neg = true;

}

}

assert(!found_neg);

positive semi-definitate 는 다음과 같은 의미를 지닌다.

positive semi-definite

이를 여기서 왜 체크해야 하는지는 정확히 모르지만, 만약 diagionals 값이 0보다 작게되면 에러라고 판단한다.

 

StateHelper::augment_clone()

        /**
         * @brief Augment the state with a stochastic copy of the current IMU pose
         *
         * After propagation, normally we augment the state with an new clone that is at the new update timestep.
         * This augmentation clones the IMU pose and adds it to our state's clone map.
         * If we are doing time offset calibration we also make our cloning a function of the time offset.
         * Time offset logic is based on Mingyang Li and Anastasios I. Mourikis paper: http://journals.sagepub.com/doi/pdf/10.1177/0278364913515286
         * We can write the current clone at the true imu base clock time as the follow:
         * \f{align*}{
         * {}^{I_{t+t_d}}_G\bar{q} &= \begin{bmatrix}\frac{1}{2} {}^{I_{t+\hat{t}_d}}\boldsymbol\omega \tilde{t}_d \\ 1\end{bmatrix}\otimes{}^{I_{t+\hat{t}_d}}_G\bar{q} \\
         * {}^G\mathbf{p}_{I_{t+t_d}} &= {}^G\mathbf{p}_{I_{t+\hat{t}_d}} + {}^G\mathbf{v}_{I_{t+\hat{t}_d}}\tilde{t}_d
         * \f}
         * where we say that we have propagated our state up to the current estimated true imaging time for the current image,
         * \f${}^{I_{t+\hat{t}_d}}\boldsymbol\omega\f$ is the angular velocity at the end of propagation with biases removed.
         * This is off by some smaller error, so to get to the true imaging time in the imu base clock, we can append some small timeoffset error.
         * Thus the Jacobian in respect to our time offset during our cloning procedure is the following:
         * \f{align*}{
         * \frac{\partial {}^{I_{t+t_d}}_G\tilde{\boldsymbol\theta}}{\partial \tilde{t}_d} &= {}^{I_{t+\hat{t}_d}}\boldsymbol\omega \\
         * \frac{\partial {}^G\tilde{\mathbf{p}}_{I_{t+t_d}}}{\partial \tilde{t}_d} &= {}^G\mathbf{v}_{I_{t+\hat{t}_d}}
         * \f}
         *
         * @param state Pointer to state
         * @param last_w The estimated angular velocity at cloning time (used to estimate imu-cam time offset)
         */
        static void augment_clone(State *state, Eigen::Matrix<double, 3, 1> last_w);
        
        void StateHelper::augment_clone(State *state, Eigen::Matrix<double, 3, 1> last_w) {

    // Call on our marginalizer to clone, it will add it to our vector of types
    // NOTE: this will clone the clone pose to the END of the covariance...
    Type *posetemp = StateHelper::clone(state, state->_imu->pose());

    // Cast to a JPL pose type
    PoseJPL *pose = dynamic_cast<PoseJPL*>(posetemp);

    // Check that it was a valid cast
    if (pose == nullptr) {
        printf(RED "INVALID OBJECT RETURNED FROM STATEHELPER CLONE, EXITING!#!@#!@#\n" RESET);
        std::exit(EXIT_FAILURE);
    }

    // Append the new clone to our clone vector
    state->_clones_IMU.insert({state->_timestamp, pose});

    // If we are doing time calibration, then our clones are a function of the time offset
    // Logic is based on Mingyang Li and Anastasios I. Mourikis paper:
    // http://journals.sagepub.com/doi/pdf/10.1177/0278364913515286
    if (state->_options.do_calib_camera_timeoffset) {
        // Jacobian to augment by
        Eigen::Matrix<double, 6, 1> dnc_dt = Eigen::MatrixXd::Zero(6, 1);
        dnc_dt.block(0, 0, 3, 1) = last_w;
        dnc_dt.block(3, 0, 3, 1) = state->_imu->vel();
        // Augment covariance with time offset Jacobian
        state->_Cov.block(0, pose->id(), state->_Cov.rows(), 6) +=
                state->_Cov.block(0, state->_calib_dt_CAMtoIMU->id(), state->_Cov.rows(), 1) * dnc_dt.transpose();
        state->_Cov.block(pose->id(), 0, 6, state->_Cov.rows()) +=
                dnc_dt * state->_Cov.block(state->_calib_dt_CAMtoIMU->id(), 0, 1, state->_Cov.rows());
        state->_Cov.block(pose->id(), pose->id(), 6, 6) +=
                dnc_dt * state->_Cov(state->_calib_dt_CAMtoIMU->id(), state->_calib_dt_CAMtoIMU->id()) * dnc_dt.transpose();
    }

}

// Call on our marginalizer to clone, it will add it to our vector of types

// NOTE: this will clone the clone pose to the END of the covariance...

Type *posetemp = StateHelper::clone(state, state->_imu->pose());

clone을 진행하여 posetemp에 담는다.

 

// Cast to a JPL pose type

PoseJPL *pose = dynamic_cast<PoseJPL*>(posetemp);

이를 PoseJPL type으로 만들어준다.

 

// Check that it was a valid cast

if (pose == nullptr) {

printf(RED "INVALID OBJECT RETURNED FROM STATEHELPER CLONE, EXITING!#!@#!@#\n" RESET);

std::exit(EXIT_FAILURE);

}

pose가 제대로 cast되었는지 확인한다.

 

// Append the new clone to our clone vector

state->_clones_IMU.insert({state->_timestamp, pose});

새로운 clone을 clone vector에 넣는다.

 

// If we are doing time calibration, then our clones are a function of the time offset

// Logic is based on Mingyang Li and Anastasios I. Mourikis paper:

// http://journals.sagepub.com/doi/pdf/10.1177/0278364913515286

if (state->_options.do_calib_camera_timeoffset) {

// Jacobian to augment by

Eigen::Matrix<double, 6, 1> dnc_dt = Eigen::MatrixXd::Zero(6, 1);

dnc_dt.block(0, 0, 3, 1) = last_w;

dnc_dt.block(3, 0, 3, 1) = state->_imu->vel();

// Augment covariance with time offset Jacobian

state->_Cov.block(0, pose->id(), state->_Cov.rows(), 6) +=

state->_Cov.block(0, state->_calib_dt_CAMtoIMU->id(), state->_Cov.rows(), 1) * dnc_dt.transpose();

state->_Cov.block(pose->id(), 0, 6, state->_Cov.rows()) +=

dnc_dt * state->_Cov.block(state->_calib_dt_CAMtoIMU->id(), 0, 1, state->_Cov.rows());

state->_Cov.block(pose->id(), pose->id(), 6, 6) +=

dnc_dt * state->_Cov(state->_calib_dt_CAMtoIMU->id(), state->_calib_dt_CAMtoIMU->id()) * dnc_dt.transpose();

}

만약 time calibration 옵션이 true라면 해당 부분을 수행해주어서 _Cov의 값들을 계산해주게 된다. 이 부분은 추후에 더 살펴보도록 하자.

페이퍼는 다음과 같다.

Mingyang Li and Anastasios I. Mourikis paper

 

 

 

StateHelper::clone()

        /**
         * @brief Clones "variable to clone" and places it at end of covariance
         * @param state Pointer to state
         * @param variable_to_clone Pointer to variable that will be cloned
         */
        static Type* clone(State *state, Type *variable_to_clone);
        
        Type* StateHelper::clone(State *state, Type *variable_to_clone) {

    //Get total size of new cloned variables, and the old covariance size
    int total_size = variable_to_clone->size();
    int old_size = (int)state->_Cov.rows();
    int new_loc = (int)state->_Cov.rows();

    // Resize both our covariance to the new size
    state->_Cov.conservativeResizeLike(Eigen::MatrixXd::Zero(old_size + total_size, old_size + total_size));

    // What is the new state, and variable we inserted
    const std::vector<Type*> new_variables = state->_variables;
    Type *new_clone = nullptr;

    // Loop through all variables, and find the variable that we are going to clone
    for (size_t k = 0; k < state->_variables.size(); k++) {

        // Skip this if it is not the same
        Type *type_check = state->_variables.at(k)->check_if_same_variable(variable_to_clone);
        if (type_check == nullptr)
            continue;

        // So we will clone this one
        int old_loc = type_check->id();

        // Copy the covariance elements
        state->_Cov.block(new_loc, new_loc, total_size, total_size) = state->_Cov.block(old_loc, old_loc, total_size, total_size);
        state->_Cov.block(0, new_loc, old_size, total_size) = state->_Cov.block(0, old_loc, old_size, total_size);
        state->_Cov.block(new_loc, 0, total_size, old_size) = state->_Cov.block(old_loc, 0, total_size, old_size);

        // Create clone from the type being cloned
        new_clone = type_check->clone();
        new_clone->set_local_id(new_loc);

        // Add to variable list
        state->_variables.push_back(new_clone);
        break;

    }

    // Check if the current state has this variable
    if (new_clone == nullptr) {
        printf(RED "StateHelper::clone() - Called on variable is not in the state\n" RESET);
        printf(RED "StateHelper::clone() - Ensure that the variable specified is a variable, or sub-variable..\n" RESET);
        std::exit(EXIT_FAILURE);
    }

    return new_clone;

}

//Get total size of new cloned variables, and the old covariance size

int total_size = variable_to_clone->size();

int old_size = (int)state->_Cov.rows();

int new_loc = (int)state->_Cov.rows();

데이터의 사이즈를 가져온다.

 

// Resize both our covariance to the new size

state->_Cov.conservativeResizeLike(Eigen::MatrixXd::Zero(old_size + total_size, old_size + total_size));

covariance matrix의 사이즈를 조정한다.

 

// What is the new state, and variable we inserted

const std::vector<Type*> new_variables = state->_variables;

Type *new_clone = nullptr;

variable 과 clone을 선언한다.

 

// Loop through all variables, and find the variable that we are going to clone

for (size_t k = 0; k < state->_variables.size(); k++) {

모든 variable에 대해 반복문을 수행한다.

 

// Skip this if it is not the same

Type *type_check = state->_variables.at(k)->check_if_same_variable(variable_to_clone);

if (type_check == nullptr)

continue;

_variables 는 많은 variables 들을 갖고 있다. 이 중 _variables.at(k) 를 통해 선택된 variable 이 variable_to_clone 과 일치하는지 확인한다. 만일 일치하지 않는다면 skip 한다.

 

// So we will clone this one

int old_loc = type_check->id();

일치한다면 해당 variable의 id를 가져온다.

 

// Copy the covariance elements

state->_Cov.block(new_loc, new_loc, total_size, total_size) = state->_Cov.block(old_loc, old_loc, total_size, total_size);

state->_Cov.block(0, new_loc, old_size, total_size) = state->_Cov.block(0, old_loc, old_size, total_size);

state->_Cov.block(new_loc, 0, total_size, old_size) = state->_Cov.block(old_loc, 0, total_size, old_size);

새로운 값들(covariance matrix에 관련된 행렬들)을 state->_Cov에 clone 시킨다. 

 

// Create clone from the type being cloned

new_clone = type_check->clone();

new_clone->set_local_id(new_loc);

type_check 에서 받아온 type에 따라서 clone() 함수를 작동시키게 되는데, 여기서는 PoseJPL::clone() 이 동작하게 되며, Current best Estimate와 variable's first-estimate를 갖고있는 clone을 가져온다.

그리고 해당 clone의 id를 set한다.

 

// Add to variable list

state->_variables.push_back(new_clone);

break;

이제 해당 clone을 state->_variables에 추가해준다.

 

// Check if the current state has this variable

if (new_clone == nullptr) {

printf(RED "StateHelper::clone() - Called on variable is not in the state\n" RESET);

printf(RED "StateHelper::clone() - Ensure that the variable specified is a variable, or sub-variable..\n" RESET);

std::exit(EXIT_FAILURE);

}

return new_clone;

만약 해당 clone이 nullptr라면 에러를 출력해준다.

그렇지 않다면 해당하는 clone을 return한다.

 

 

[Type::IMU] state->_variables.at(k)->check_if_same_variable(variable_to_clone)

파라미터로 들어오는 type이 _variables.at(k) 와 일치하는지 확인한다. 

일치한다면 해당 variable의 주소를 반환한다.

        /**
         * @brief Determine if "check" is the same variable
         * If the passed variable is a sub-variable or the current variable this will return it.
         * Otherwise it will return a nullptr, meaning that it was unable to be found.
         *
         * @param check Type pointer to compare to
         */
        virtual Type *check_if_same_variable(const Type *check) {
            if (check == this) {
                return this;
            } else {
                return nullptr;
            }
        }

 

[Type::PoseJPL] type_check->clone()

다음과 같은 함수들이 동작해서, Current best Estimate와 variable's first-estimate를 set한다.

        Type *clone() override {
            Type *Clone = new PoseJPL();
            Clone->set_value(value());
            Clone->set_fej(fej());
            return Clone;
        }
        
        
        
         /**
         * @brief Overwrite value of state's estimate
         * @param new_value New value that will overwrite state's value
         */
        virtual void set_value(const Eigen::MatrixXd new_value) {
            assert(_value.rows()==new_value.rows());
            assert(_value.cols()==new_value.cols());
            _value = new_value;
        }

        /**
         * @brief Overwrite value of first-estimate
         * @param new_value New value that will overwrite state's fej
         */
        virtual void set_fej(const Eigen::MatrixXd new_value) {
            assert(_fej.rows()==new_value.rows());
            assert(_fej.cols()==new_value.cols());
            _fej = new_value;
        }
        
        
        
        
         /**
         * @brief Access variable's estimate
         */
        virtual Eigen::MatrixXd value() const {
            return _value;
        }
        
         /**
         * @brief Access variable's first-estimate
         */
        virtual Eigen::MatrixXd fej() const {
            return _fej;
        }

 

[Type] new_clone->set_local_id()

해당 clone의 id를 set한다.

        /**
         * @brief Sets id used to track location of variable in the filter covariance
         *
         * Note that we update the sub-variables also.
         *
         * @param new_id entry in filter covariance corresponding to this variable
         */
        void set_local_id(int new_id) override {
            _id = new_id;
            _q->set_local_id(new_id);
            _p->set_local_id(new_id+_q->size());
        }

        /**
        * @brief Sets id used to track location of variable in the filter covariance
         *
        * @param new_id entry in filter covariance corresponding to this variable
        */
        virtual void set_local_id(int new_id) {
            _id = new_id;
        }
        
        /// Location of error state in covariance
        int _id = -1;

 

 

trackFEATS->get_feature_database()->features_not_containing_newer()

 

        /**
         * @brief Get features that do not have newer measurement then the specified time.
         *
         * This function will return all features that do not a measurement at a time greater than the specified time.
         * For example this could be used to get features that have not been successfully tracked into the newest frame.
         * All features returned will not have any measurements occurring at a time greater then the specified.
         */
        std::vector<Feature *> features_not_containing_newer(double timestamp, bool remove=false) {

            // Our vector of features that do not have measurements after the specified time
            std::vector<Feature *> feats_old;

            // Now lets loop through all features, and just make sure they are not old
            std::unique_lock<std::mutex> lck(mtx);
            for (auto it = features_idlookup.begin(); it != features_idlookup.end();) {
                // Loop through each camera
                bool has_newer_measurement = false;
                for (auto const &pair : (*it).second->timestamps) {
                    // If we have a measurement greater-than or equal to the specified, this measurement is find
                    if (!pair.second.empty() && pair.second.at(pair.second.size() - 1) >= timestamp) {
                        has_newer_measurement = true;
                        break;
                    }
                }
                // If it is not being actively tracked, then it is old
                if (!has_newer_measurement) {
                    feats_old.push_back((*it).second);
                    if(remove) features_idlookup.erase(it++);
                    else it++;
                } else {
                    it++;
                }
            }

            // Debugging
            //std::cout << "feature db size = " << features_idlookup.size() << std::endl;

            // Return the old features
            return feats_old;

        }

// Our vector of features that do not have measurements after the specified time

std::vector<Feature *> feats_old;

선언

 

// Now lets loop through all features, and just make sure they are not old

std::unique_lock<std::mutex> lck(mtx);

for (auto it = features_idlookup.begin(); it != features_idlookup.end();) {

모든 features에 대한 반복문

 

// Loop through each camera

bool has_newer_measurement = false;

for (auto const &pair : (*it).second->timestamps) {

각 카메라에 대해 수행, 우리 시스템에서는 하나의 카메라에 대해 수행.

 

it 는 features_idlookup 을 의미하고 여기서 second 는 "Feat" 를 의미한다.

Feat의 clean_older_measurements 함수를 수행하는 것이다.

이 때, timestamp를 매개변수로 쓰게 되는데 이는 현재 시간에 대한 정보이다.

 

timestamps의 원형은 다음과 같다.

 

/// Timestamps of each UV measurement (mapped by camera ID)

std::unordered_map<size_t, std::vector<double>> timestamps;

 

그러므로 (*it).second->timestamps 를 반복문으로 돌린다는 것은 

unordered_map 을 대상으로 돌린다는 것이고,

stereo camera의 경우에는 2번 돌리겠지만,

mono camera의 경우에는 1번만 돌아갈 것이다.

 

size_t에는 camera ID가 들어가고 std::vector<double> 에는 time 들이 vector 형으로 기록되게 된다. 

 

이러한 timestamps 의 주소를 pair 로 가져오게 되는 것이고, 

pair.first 는 camera ID 가 되는 것이다. 

 

// If we have a measurement greater-than or equal to the specified, this measurement is find

if (!pair.second.empty() && pair.second.at(pair.second.size() - 1) >= timestamp) {

has_newer_measurement = true;

break;

}

pair.second(features)가 비어있지 않고 그 시간이 특정 timestamp보다 크다면 새로운 feature가 발견된 것이므로 flag를 true로 바꾸고 반복문을 멈춘다.

 

// If it is not being actively tracked, then it is old

if (!has_newer_measurement) {

feats_old.push_back((*it).second);

if(remove) features_idlookup.erase(it++);

else it++;

} else {

it++;

}

만약 old data라면 feats_old에 담고,

remove flag에 따라 features_idlookup을 지우거나 남겨둔다.

그리고 iterator를 증가시켜 준다.

내 생각에 이렇게 하는 이유는, unordered_map 구조의 특성상 순차적으로 데이터가 정해지지 않기 때문에 모든 데이터를 확인하려 그런 것 같다.

 

// Return the old features

return feats_old;

얻어진 feats_old를 return 한다.

 

State::margtimestep()

marginalize 할 clone의 time을 반환하는 함수인데, 여기서는 clone 중에 가장 오래된 값(첫번째 값)을 반환한다.

        /**
         * @brief Will return the timestep that we will marginalize next.
         * As of right now, since we are using a sliding window, this is the oldest clone.
         * But if you wanted to do a keyframe system, you could selectively marginalize clones.
         * @return timestep of clone we will marginalize
         */
        double margtimestep() {
            double time = INFINITY;
            for (std::pair<const double, PoseJPL*> &clone_imu : _clones_IMU) {
                if (clone_imu.first < time) {
                    time = clone_imu.first;
                }
            }
            return time;
        }

 

 

 

features_containing()

        /**
         * @brief Get features that has measurements at the specified time.
         *
         * This function will return all features that have the specified time in them.
         * This would be used to get all features that occurred at a specific clone/state.
         */
        std::vector<Feature *> features_containing(double timestamp, bool remove=false) {

            // Our vector of old features
            std::vector<Feature *> feats_has_timestamp;

            // Now lets loop through all features, and just make sure they are not
            std::unique_lock<std::mutex> lck(mtx);
            for (auto it = features_idlookup.begin(); it != features_idlookup.end();) {
                // Boolean if it has the timestamp
                bool has_timestamp = false;
                for (auto const &pair : (*it).second->timestamps) {
                    // Loop through all timestamps, and see if it has it
                    for (auto &timefeat : pair.second) {
                        if (timefeat == timestamp) {
                            has_timestamp = true;
                            break;
                        }
                    }
                    // Break out if we found a single timestamp that is equal to the specified time
                    if (has_timestamp) {
                        break;
                    }
                }
                // Remove this feature if it contains the specified timestamp
                if (has_timestamp) {
                    feats_has_timestamp.push_back((*it).second);
                    if(remove) features_idlookup.erase(it++);
                    else it++;
                } else {
                    it++;
                }
            }

            // Debugging
            //std::cout << "feature db size = " << features_idlookup.size() << std::endl;
            //std::cout << "return vector = " << feats_has_timestamp.size() << std::endl;

            // Return the features
            return feats_has_timestamp;

        }

// Our vector of old features

std::vector<Feature *> feats_has_timestamp;

선언

 

// Now lets loop through all features, and just make sure they are not

std::unique_lock<std::mutex> lck(mtx);

for (auto it = features_idlookup.begin(); it != features_idlookup.end();) {

// Boolean if it has the timestamp

bool has_timestamp = false;

for (auto const &pair : (*it).second->timestamps) {

// Loop through all timestamps, and see if it has it

for (auto &timefeat : pair.second) {

if (timefeat == timestamp) {

has_timestamp = true;

break;

}

}

// Break out if we found a single timestamp that is equal to the specified time

if (has_timestamp) {

break;

}

}

// Remove this feature if it contains the specified timestamp

if (has_timestamp) {

feats_has_timestamp.push_back((*it).second);

if(remove) features_idlookup.erase(it++);

else it++;

} else {

it++;

}

}

위의 features_containing_older() 와 크게 다르지 않기 때문에 넘어가겠다.

 

// Return the features

return feats_has_timestamp;

현재 timestamp와 같은 데이터를 반환한다.

 

get_feature()

해당 id의 feature를 반환한다. (없다면 nullptr 반환)

        /**
         * @brief Get a specified feature
         * @param id What feature we want to get
         * @param remove Set to true if you want to remove the feature from the database (you will need to handle the freeing of memory)
         * @return Either a feature object, or null if it is not in the database.
         */
        Feature *get_feature(size_t id, bool remove=false) {
            std::unique_lock<std::mutex> lck(mtx);
            if (features_idlookup.find(id) != features_idlookup.end()) {
                Feature* temp = features_idlookup[id];
                if(remove) features_idlookup.erase(id);
                return temp;
            } else {
                return nullptr;
            }
        }

 

marginalize_slam()

marginalize flag가 true인 feature SLAM 들을 제거해준다.

        /**
         * @brief Marginalize bad SLAM features
         * @param state Pointer to state
         */
        static void marginalize_slam(State* state) {
            // Remove SLAM features that have their marginalization flag set
            // We also check that we do not remove any aruoctag landmarks
            auto it0 = state->_features_SLAM.begin();
            while(it0 != state->_features_SLAM.end()) {
                if((*it0).second->should_marg && (int)(*it0).first > state->_options.max_aruco_features) {
                    StateHelper::marginalize(state, (*it0).second);
                    it0 = state->_features_SLAM.erase(it0);
                } else {
                    it0++;
                }
            }
        }

 

StateHelper::marginalize()

        /**
         * @brief Marginalizes a variable, properly modifying the ordering/covariances in the state
         *
         * This function can support any Type variable out of the box.
         * Right now the marginalization of a sub-variable/type is not supported.
         * For example if you wanted to just marginalize the orientation of a PoseJPL, that isn't supported.
         * We will first remove the rows and columns corresponding to the type (i.e. do the marginalization).
         * After we update all the type ids so that they take into account that the covariance has shrunk in parts of it.
         *
         * @param state Pointer to state
         * @param marg Pointer to variable to marginalize
         */
        static void marginalize(State *state, Type *marg);
        
        void StateHelper::marginalize(State *state, Type *marg) {

    // Check if the current state has the element we want to marginalize
    if (std::find(state->_variables.begin(), state->_variables.end(), marg) == state->_variables.end()) {
        printf(RED "StateHelper::marginalize() - Called on variable that is not in the state\n" RESET);
        printf(RED "StateHelper::marginalize() - Marginalization, does NOT work on sub-variables yet...\n" RESET);
        std::exit(EXIT_FAILURE);
    }

    //Generic covariance has this form for x_1, x_m, x_2. If we want to remove x_m:
    //
    //  P_(x_1,x_1) P(x_1,x_m) P(x_1,x_2)
    //  P_(x_m,x_1) P(x_m,x_m) P(x_m,x_2)
    //  P_(x_2,x_1) P(x_2,x_m) P(x_2,x_2)
    //
    //  to
    //
    //  P_(x_1,x_1) P(x_1,x_2)
    //  P_(x_2,x_1) P(x_2,x_2)
    //
    // i.e. x_1 goes from 0 to marg_id, x_2 goes from marg_id+marg_size to Cov.rows() in the original covariance

    int marg_size = marg->size();
    int marg_id = marg->id();
    int x2_size = (int)state->_Cov.rows() - marg_id - marg_size;

    Eigen::MatrixXd Cov_new(state->_Cov.rows() - marg_size, state->_Cov.rows() - marg_size);

    //P_(x_1,x_1)
    Cov_new.block(0, 0, marg_id, marg_id) = state->_Cov.block(0, 0, marg_id, marg_id);

    //P_(x_1,x_2)
    Cov_new.block(0, marg_id, marg_id, x2_size) = state->_Cov.block(0, marg_id + marg_size, marg_id, x2_size);

    //P_(x_2,x_1)
    Cov_new.block(marg_id, 0, x2_size, marg_id) = Cov_new.block(0, marg_id, marg_id, x2_size).transpose();

    //P(x_2,x_2)
    Cov_new.block(marg_id, marg_id, x2_size, x2_size) = state->_Cov.block(marg_id + marg_size, marg_id + marg_size, x2_size, x2_size);


    // Now set new covariance
    state->_Cov = Cov_new;
    //state->Cov() = 0.5*(Cov_new+Cov_new.transpose());
    assert(state->_Cov.rows() == Cov_new.rows());

    // Now we keep the remaining variables and update their ordering
    // Note: DOES NOT SUPPORT MARGINALIZING SUBVARIABLES YET!!!!!!!
    std::vector<Type *> remaining_variables;
    for (size_t i = 0; i < state->_variables.size(); i++) {
        // Only keep non-marginal states
        if (state->_variables.at(i) != marg) {
            if (state->_variables.at(i)->id() > marg_id) {
                // If the variable is "beyond" the marginal one in ordering, need to "move it forward"
                state->_variables.at(i)->set_local_id(state->_variables.at(i)->id() - marg_size);
            }
            remaining_variables.push_back(state->_variables.at(i));
        }
    }

    // Delete the old state variable to free up its memory
    delete marg;

    // Now set variables as the remaining ones
    state->_variables = remaining_variables;

}

// Check if the current state has the element we want to marginalize

if (std::find(state->_variables.begin(), state->_variables.end(), marg) == state->_variables.end()) {

printf(RED "StateHelper::marginalize() - Called on variable that is not in the state\n" RESET);

printf(RED "StateHelper::marginalize() - Marginalization, does NOT work on sub-variables yet...\n" RESET);

std::exit(EXIT_FAILURE);

}

unordered_map은 hash_map 구조를 갖는 데이터 형이며,

key와 value 값을 갖는 데이터들을 빠르게 검색할 수 있다는 특징을 지닌다.

 

std::unordered_map::find 함수는 파라미터로 주어지는 key 값을 찾는 iterator이며,

해당 key 값을 찾았을 때는 해당 key 값과 매칭되는 value를 반환하게 되고, 찾지 못했을 경우는
std::unordered_map::end 를 반환하게 된다. 

 

if (std::find(state->_variables.begin(), state->_variables.end(), marg) == state->_variables.end()) 는

key 값이 존재하지 않는 경우에 작동하여 에러를 출력하는 조건문이라고 보면 된다.

 

//Generic covariance has this form for x_1, x_m, x_2. If we want to remove x_m:

//

// P_(x_1,x_1) P(x_1,x_m) P(x_1,x_2)

// P_(x_m,x_1) P(x_m,x_m) P(x_m,x_2)

// P_(x_2,x_1) P(x_2,x_m) P(x_2,x_2)

//

// to

//

// P_(x_1,x_1) P(x_1,x_2)

// P_(x_2,x_1) P(x_2,x_2)

//

// i.e. x_1 goes from 0 to marg_id, x_2 goes from marg_id+marg_size to Cov.rows() in the original covariance

해당 주석처럼 우리가 SLAM marginalization을 진행하게 되면 covatiance matrix의 사이즈를 하나씩 줄이게 되는 것이므로 참고한다.

 

int marg_size = marg->size();

int marg_id = marg->id();

int x2_size = (int)state->_Cov.rows() - marg_id - marg_size;

Eigen::MatrixXd Cov_new(state->_Cov.rows() - marg_size, state->_Cov.rows() - marg_size);

marginalization이 진행되고 새롭게 만들어질 Matrix를 만든다. (rows, cols 가 한칸씩 줄어들어있는 것을 확인할 수 있다.

 

//P_(x_1,x_1)

Cov_new.block(0, 0, marg_id, marg_id) = state->_Cov.block(0, 0, marg_id, marg_id);

//P_(x_1,x_2)

Cov_new.block(0, marg_id, marg_id, x2_size) = state->_Cov.block(0, marg_id + marg_size, marg_id, x2_size);

//P_(x_2,x_1)

Cov_new.block(marg_id, 0, x2_size, marg_id) = Cov_new.block(0, marg_id, marg_id, x2_size).transpose();

//P(x_2,x_2)

Cov_new.block(marg_id, marg_id, x2_size, x2_size) = state->_Cov.block(marg_id + marg_size, marg_id + marg_size, x2_size, x2_size);

위에서 보았던 주석과 같이 작업하여준다.

 

// Now set new covariance

state->_Cov = Cov_new;

//state->Cov() = 0.5*(Cov_new+Cov_new.transpose());

assert(state->_Cov.rows() == Cov_new.rows());

이제 state->_Cov 를 수정해주고 사이즈 체크도 진행한다.

 

// Now we keep the remaining variables and update their ordering

// Note: DOES NOT SUPPORT MARGINALIZING SUBVARIABLES YET!!!!!!!

std::vector<Type *> remaining_variables;

for (size_t i = 0; i < state->_variables.size(); i++) {

// Only keep non-marginal states

if (state->_variables.at(i) != marg) {

if (state->_variables.at(i)->id() > marg_id) {

// If the variable is "beyond" the marginal one in ordering, need to "move it forward"

state->_variables.at(i)->set_local_id(state->_variables.at(i)->id() - marg_size);

}

remaining_variables.push_back(state->_variables.at(i));

}

}

이제 variable을 관리해준다.

만약 variable의 id가 marg_id 보다 크다면 앞으로 이동시켜준다.

그리고 remaining_variables에 담아준다.

 

// Delete the old state variable to free up its memory

delete marg;

이제 marg state는 제거하여 메모리를 관리해준다.

 

// Now set variables as the remaining ones

state->_variables = remaining_variables;

이제 remaining_variables를 state->_variables로 만든다.

 

[UdaterMSCKF] updaterMSCKF->update()

track된 feature를 이용해서 state를  update한다.

        /**
         * @brief Given tracked features, this will try to use them to update the state.
         *
         * @param state State of the filter
         * @param feature_vec Features that can be used for update
         */
        void update(State *state, std::vector<Feature*>& feature_vec);

void UpdaterMSCKF::update(State *state, std::vector<Feature*>& feature_vec) {

    // Return if no features
    if(feature_vec.empty())
        return;

    // Start timing
    boost::posix_time::ptime rT0, rT1, rT2, rT3, rT4, rT5, rT6, rT7;
    rT0 =  boost::posix_time::microsec_clock::local_time();

    // 0. Get all timestamps our clones are at (and thus valid measurement times)
    std::vector<double> clonetimes;
    for(const auto& clone_imu : state->_clones_IMU) {
        clonetimes.emplace_back(clone_imu.first);
    }


    // 1. Clean all feature measurements and make sure they all have valid clone times
    auto it0 = feature_vec.begin();
    while(it0 != feature_vec.end()) {

        // Clean the feature
        (*it0)->clean_old_measurements(clonetimes);

        // Count how many measurements
        int ct_meas = 0;
        for(const auto &pair : (*it0)->timestamps) {
            ct_meas += (*it0)->timestamps[pair.first].size();
        }

        // Remove if we don't have enough
        if(ct_meas < 3) {
            (*it0)->to_delete = true;
            it0 = feature_vec.erase(it0);
        } else {
            it0++;
        }

    }
    rT1 =  boost::posix_time::microsec_clock::local_time();

    // 2. Create vector of cloned *CAMERA* poses at each of our clone timesteps
    std::unordered_map<size_t, std::unordered_map<double, FeatureInitializer::ClonePose>> clones_cam;
    for(const auto &clone_calib : state->_calib_IMUtoCAM) {

        // For this camera, create the vector of camera poses
        std::unordered_map<double, FeatureInitializer::ClonePose> clones_cami;
        for(const auto &clone_imu : state->_clones_IMU) {

            // Get current camera pose
            Eigen::Matrix<double,3,3> R_GtoCi = clone_calib.second->Rot()*clone_imu.second->Rot();
            Eigen::Matrix<double,3,1> p_CioinG = clone_imu.second->pos() - R_GtoCi.transpose()*clone_calib.second->pos();

            // Append to our map
            clones_cami.insert({clone_imu.first,FeatureInitializer::ClonePose(R_GtoCi,p_CioinG)});

        }

        // Append to our map
        clones_cam.insert({clone_calib.first,clones_cami});

    }

    // 3. Try to triangulate all MSCKF or new SLAM features that have measurements
    auto it1 = feature_vec.begin();
    while(it1 != feature_vec.end()) {

        // Triangulate the feature and remove if it fails
        bool success = initializer_feat->single_triangulation(*it1, clones_cam);
        if(!success) {
            (*it1)->to_delete = true;
            it1 = feature_vec.erase(it1);
            continue;
        }

        // Gauss-newton refine the feature
        success = initializer_feat->single_gaussnewton(*it1, clones_cam);
        if(!success) {
            (*it1)->to_delete = true;
            it1 = feature_vec.erase(it1);
            continue;
        }
        it1++;

    }
    rT2 =  boost::posix_time::microsec_clock::local_time();


    // Calculate the max possible measurement size
    size_t max_meas_size = 0;
    for(size_t i=0; i<feature_vec.size(); i++) {
        for (const auto &pair : feature_vec.at(i)->timestamps) {
            max_meas_size += 2*feature_vec.at(i)->timestamps[pair.first].size();
        }
    }

    // Calculate max possible state size (i.e. the size of our covariance)
    // NOTE: that when we have the single inverse depth representations, those are only 1dof in size
    size_t max_hx_size = state->max_covariance_size();
    for(auto &landmark : state->_features_SLAM) {
        max_hx_size -= landmark.second->size();
    }

    // Large Jacobian and residual of *all* features for this update
    Eigen::VectorXd res_big = Eigen::VectorXd::Zero(max_meas_size);
    Eigen::MatrixXd Hx_big = Eigen::MatrixXd::Zero(max_meas_size, max_hx_size);
    std::unordered_map<Type*,size_t> Hx_mapping;
    std::vector<Type*> Hx_order_big;
    size_t ct_jacob = 0;
    size_t ct_meas = 0;


    // 4. Compute linear system for each feature, nullspace project, and reject
    auto it2 = feature_vec.begin();
    while(it2 != feature_vec.end()) {

        // Convert our feature into our current format
        UpdaterHelper::UpdaterHelperFeature feat;
        feat.featid = (*it2)->featid;
        feat.uvs = (*it2)->uvs;
        feat.uvs_norm = (*it2)->uvs_norm;
        feat.timestamps = (*it2)->timestamps;

        // If we are using single inverse depth, then it is equivalent to using the msckf inverse depth
        feat.feat_representation = state->_options.feat_rep_msckf;
        if(state->_options.feat_rep_msckf==LandmarkRepresentation::Representation::ANCHORED_INVERSE_DEPTH_SINGLE) {
            feat.feat_representation = LandmarkRepresentation::Representation::ANCHORED_MSCKF_INVERSE_DEPTH;
        }

        // Save the position and its fej value
        if(LandmarkRepresentation::is_relative_representation(feat.feat_representation)) {
            feat.anchor_cam_id = (*it2)->anchor_cam_id;
            feat.anchor_clone_timestamp = (*it2)->anchor_clone_timestamp;
            feat.p_FinA = (*it2)->p_FinA;
            feat.p_FinA_fej = (*it2)->p_FinA;
        } else {
            feat.p_FinG = (*it2)->p_FinG;
            feat.p_FinG_fej = (*it2)->p_FinG;
        }

        // Our return values (feature jacobian, state jacobian, residual, and order of state jacobian)
        Eigen::MatrixXd H_f;
        Eigen::MatrixXd H_x;
        Eigen::VectorXd res;
        std::vector<Type*> Hx_order;

        // Get the Jacobian for this feature
        UpdaterHelper::get_feature_jacobian_full(state, feat, H_f, H_x, res, Hx_order);

        // Nullspace project
        UpdaterHelper::nullspace_project_inplace(H_f, H_x, res);

        /// Chi2 distance check
        Eigen::MatrixXd P_marg = StateHelper::get_marginal_covariance(state, Hx_order);
        Eigen::MatrixXd S = H_x*P_marg*H_x.transpose();
        S.diagonal() += _options.sigma_pix_sq*Eigen::VectorXd::Ones(S.rows());
        double chi2 = res.dot(S.llt().solve(res));

        // Get our threshold (we precompute up to 500 but handle the case that it is more)
        double chi2_check;
        if(res.rows() < 500) {
            chi2_check = chi_squared_table[res.rows()];
        } else {
            boost::math::chi_squared chi_squared_dist(res.rows());
            chi2_check = boost::math::quantile(chi_squared_dist, 0.95);
            printf(YELLOW "chi2_check over the residual limit - %d\n" RESET, (int)res.rows());
        }

        // Check if we should delete or not
        if(chi2 > _options.chi2_multipler*chi2_check) {
            (*it2)->to_delete = true;
            it2 = feature_vec.erase(it2);
            //cout << "featid = " << feat.featid << endl;
            //cout << "chi2 = " << chi2 << " > " << _options.chi2_multipler*chi2_check << endl;
            //cout << "res = " << endl << res.transpose() << endl;
            continue;
        }

        // We are good!!! Append to our large H vector
        size_t ct_hx = 0;
        for(const auto &var : Hx_order) {

            // Ensure that this variable is in our Jacobian
            if(Hx_mapping.find(var)==Hx_mapping.end()) {
                Hx_mapping.insert({var,ct_jacob});
                Hx_order_big.push_back(var);
                ct_jacob += var->size();
            }

            // Append to our large Jacobian
            Hx_big.block(ct_meas,Hx_mapping[var],H_x.rows(),var->size()) = H_x.block(0,ct_hx,H_x.rows(),var->size());
            ct_hx += var->size();

        }

        // Append our residual and move forward
        res_big.block(ct_meas,0,res.rows(),1) = res;
        ct_meas += res.rows();
        it2++;

    }
    rT3 =  boost::posix_time::microsec_clock::local_time();

    // We have appended all features to our Hx_big, res_big
    // Delete it so we do not reuse information
    for (size_t f=0; f < feature_vec.size(); f++) {
        feature_vec[f]->to_delete = true;
    }

    // Return if we don't have anything and resize our matrices
    if(ct_meas < 1) {
        return;
    }
    assert(ct_meas<=max_meas_size);
    assert(ct_jacob<=max_hx_size);
    res_big.conservativeResize(ct_meas,1);
    Hx_big.conservativeResize(ct_meas,ct_jacob);


    // 5. Perform measurement compression
    UpdaterHelper::measurement_compress_inplace(Hx_big, res_big);
    if(Hx_big.rows() < 1) {
        return;
    }
    rT4 =  boost::posix_time::microsec_clock::local_time();


    // Our noise is isotropic, so make it here after our compression
    Eigen::MatrixXd R_big = _options.sigma_pix_sq*Eigen::MatrixXd::Identity(res_big.rows(),res_big.rows());

    // 6. With all good features update the state
    StateHelper::EKFUpdate(state, Hx_order_big, Hx_big, res_big, R_big);
    rT5 =  boost::posix_time::microsec_clock::local_time();

    // Debug print timing information
    //printf("[MSCKF-UP]: %.4f seconds to clean\n",(rT1-rT0).total_microseconds() * 1e-6);
    //printf("[MSCKF-UP]: %.4f seconds to triangulate\n",(rT2-rT1).total_microseconds() * 1e-6);
    //printf("[MSCKF-UP]: %.4f seconds create system (%d features)\n",(rT3-rT2).total_microseconds() * 1e-6, (int)feature_vec.size());
    //printf("[MSCKF-UP]: %.4f seconds compress system\n",(rT4-rT3).total_microseconds() * 1e-6);
    //printf("[MSCKF-UP]: %.4f seconds update state (%d size)\n",(rT5-rT4).total_microseconds() * 1e-6, (int)res_big.rows());
    //printf("[MSCKF-UP]: %.4f seconds total\n",(rT5-rT1).total_microseconds() * 1e-6);

}

 

// Return if no features

if(feature_vec.empty())

return;

 일단 feature vector 에 값이 있는지 확인한다.

 

// Start timing

boost::posix_time::ptime rT0, rT1, rT2, rT3, rT4, rT5, rT6, rT7;

rT0 = boost::posix_time::microsec_clock::local_time();

 시간 체크

 

// 0. Get all timestamps our clones are at (and thus valid measurement times)

std::vector<double> clonetimes;

for(const auto& clone_imu : state->_clones_IMU) {

clonetimes.emplace_back(clone_imu.first);

}

 clonetimes vector에 _clones_IMU의 모든 timestamp를 받아온다.

 

// 1. Clean all feature measurements and make sure they all have valid clone times

auto it0 = feature_vec.begin();

while(it0 != feature_vec.end()) {

 feature_vec 에 대한 iterator를 만들어 반복문을 돌린다.

// Clean the feature

(*it0)->clean_old_measurements(clonetimes);

 clonetimes vector의 timestamp에 해당하지 않는 features들은 clean_old_measurements() 함수를 이용해 지워준다.

 

// Count how many measurements

int ct_meas = 0;

for(const auto &pair : (*it0)->timestamps) {

ct_meas += (*it0)->timestamps[pair.first].size();

}

timestamps의 원형은 다음과 같다.

/// Timestamps of each UV measurement (mapped by camera ID)

std::unordered_map<size_t, std::vector<double>> timestamps;

 

그러므로 (*it)->timestamps 를 반복문으로 돌린다는 것은 

unordered_map 을 대상으로 돌린다는 것이고,

stereo camera의 경우에는 2번 돌리겠지만,

mono camera의 경우에는 1번만 돌아갈 것이다.

 

size_t에는 camera ID가 들어가고 std::vector<double> 에는 time 들이 vector 형으로 기록되게 된다. 

 

이러한 timestamps 의 주소를 pair 로 가져오게 되는 것이고, 

pair.first 는 camera ID 가 되는 것이다. 

 

(*it0)->timestamps[pair.first].size()는 해당하는 camera id 안에 몇개의 timestamp 데이터가 존재하는지를 구하는 것이다.

 

// Remove if we don't have enough

if(ct_meas < 3) {

(*it0)->to_delete = true;

it0 = feature_vec.erase(it0);

} else {

it0++;

}

 만약 clone imu의 timestamp 중 하나의 features의 개수가 3개가 안된다면 그냥 지워버리게 된다.

 

rT1 = boost::posix_time::microsec_clock::local_time();

 끝 시간 측정

 

// 2. Create vector of cloned *CAMERA* poses at each of our clone timesteps

std::unordered_map<size_t, std::unordered_map<double, FeatureInitializer::ClonePose>> clones_cam;

for(const auto &clone_calib : state->_calib_IMUtoCAM) {

 clone timestaps에서의 camera poses에 대한 vector를 생성하게 된다.

state->_calib_IMUtoCAM의 원형은 다음과 같다.

 

/// Calibration poses for each camera (R_ItoC, p_IinC)

std::unordered_map<size_t, PoseJPL*> _calib_IMUtoCAM;

 

이는 IMU와 CAM간의 외부 캘리브레이션 값인데, 이는 카메라 개수에 따라 달라지기에 반복문으로 처리하는 것이다. 우리 시스템에서 카메라는 한대이기 때문에 한 대에 대한 값만 처리하면 된다.

 

// For this camera, create the vector of camera poses

std::unordered_map<double, FeatureInitializer::ClonePose> clones_cami;

for(const auto &clone_imu : state->_clones_IMU) {

해당 카메라를 위한 clones_cam을 만든다. 이를 _clones_IMU의 데이터들과 맞춰주기 위함이다.

 

// Get current camera pose

Eigen::Matrix<double,3,3> R_GtoCi = clone_calib.second->Rot()*clone_imu.second->Rot();

Eigen::Matrix<double,3,1> p_CioinG = clone_imu.second->pos() - R_GtoCi.transpose()*clone_calib.second->pos();

R_GtoCi는 IMU와 CAM의 외부 캘리브레이션의 회전 행렬과 imu clone의 회전 행렬값을 곱해줌으로써 카메라의 회전행렬을 얻어주었다고 보면 된다.

즉, camera가 얼만큼 회전했는지를 의미한다.

 

이러한 R_GtoCi를 camera와 imu의 position 관계를 의미하는 clone_calib.second->pos() 에 곱하게 되면,

camera가 imu로부터 얼마나 떨어져있고, 얼마나 회전한 상태인지 알 수 있고,

최종적으로 이를 clone_imu의 position에서 빼면 global map 안에서 camera의 위치를 알 수 있게 되는 것이다.

 

조잡한 그림으로 나타내보자면 다음과 같다...

 

 

// Append to our map

clones_cami.insert({clone_imu.first,FeatureInitializer::ClonePose(R_GtoCi,p_CioinG)});

 이제 해당 정보를 clones_cami에 넣는다.

clone_imu.first는 시간이 된다.

 

// Append to our map

clones_cam.insert({clone_calib.first,clones_cami});

 이를 map에 담는다.

clone_calib.first는 camera이다.

 

// 3. Try to triangulate all MSCKF or new SLAM features that have measurements

auto it1 = feature_vec.begin();

while(it1 != feature_vec.end()) {

 이제 모든 feature에 대해 triangulation을 수행한다.

 

// Triangulate the feature and remove if it fails

bool success = initializer_feat->single_triangulation(*it1, clones_cam);

if(!success) {

(*it1)->to_delete = true;

it1 = feature_vec.erase(it1);

continue;

}

 initializer_feat->single_triangulation() 함수를 통해서 "a solvable linear system that can give us an initial guess for the 3D position of our feature" 을 만드는 것으로 보면 된다.

 

// Gauss-newton refine the feature

success = initializer_feat->single_gaussnewton(*it1, clones_cam);

if(!success) {

(*it1)->to_delete = true;

it1 = feature_vec.erase(it1);

continue;

}

it1++;

이제 single_gaussnewton() 함수를 이용해 더 정확도가 높은 solvable linear system을 얻어냄.

 

rT2 = boost::posix_time::microsec_clock::local_time();

시간 체크

 

// Calculate the max possible measurement size

size_t max_meas_size = 0;

for(size_t i=0; i<feature_vec.size(); i++) {

for (const auto &pair : feature_vec.at(i)->timestamps) {

max_meas_size += 2*feature_vec.at(i)->timestamps[pair.first].size();

}

}

보류.

 

// Calculate max possible state size (i.e. the size of our covariance)

// NOTE: that when we have the single inverse depth representations, those are only 1dof in size

size_t max_hx_size = state->max_covariance_size();

for(auto &landmark : state->_features_SLAM) {

max_hx_size -= landmark.second->size();

}

 _features_SLAM에서 landmark들을 가져옴.

 

// Large Jacobian and residual of *all* features for this update

Eigen::VectorXd res_big = Eigen::VectorXd::Zero(max_meas_size);

Eigen::MatrixXd Hx_big = Eigen::MatrixXd::Zero(max_meas_size, max_hx_size);

std::unordered_map<Type*,size_t> Hx_mapping;

std::vector<Type*> Hx_order_big;

size_t ct_jacob = 0;

size_t ct_meas = 0;

 update를 위한 모든 features의 vector와 matrix를 만듦. 

 

// 4. Compute linear system for each feature, nullspace project, and reject

auto it2 = feature_vec.begin();

while(it2 != feature_vec.end()) {

 모든 feature에 대해 반복문 진행.

 

// Convert our feature into our current format

UpdaterHelper::UpdaterHelperFeature feat;

feat.featid = (*it2)->featid;

feat.uvs = (*it2)->uvs;

feat.uvs_norm = (*it2)->uvs_norm;

feat.timestamps = (*it2)->timestamps;

 모든 변수들을 가져옴.

 

// If we are using single inverse depth, then it is equivalent to using the msckf inverse depth

feat.feat_representation = state->_options.feat_rep_msckf;

if(state->_options.feat_rep_msckf==LandmarkRepresentation::Representation::ANCHORED_INVERSE_DEPTH_SINGLE) {

feat.feat_representation = LandmarkRepresentation::Representation::ANCHORED_MSCKF_INVERSE_DEPTH;

}

 landmark를 어떻게 표현할지에 대한 결정. Doc에 자세히 나와있음.

우리는 GLOBAL_3D 를 사용함.

 

// Save the position and its fej value

if(LandmarkRepresentation::is_relative_representation(feat.feat_representation)) {

feat.anchor_cam_id = (*it2)->anchor_cam_id;

feat.anchor_clone_timestamp = (*it2)->anchor_clone_timestamp;

feat.p_FinA = (*it2)->p_FinA;

feat.p_FinA_fej = (*it2)->p_FinA;

} else {

feat.p_FinG = (*it2)->p_FinG;

feat.p_FinG_fej = (*it2)->p_FinG;

}

 representation 방법에 따라 구분되는데, 우리는 GLOBAL_3D를 사용하므로 else 부분을 보면 됨.

features들의 Ground에서 위치를 의미하는 p_FinG를 받아옴.

 

 

 

// Our return values (feature jacobian, state jacobian, residual, and order of state jacobian)

Eigen::MatrixXd H_f;

Eigen::MatrixXd H_x;

Eigen::VectorXd res;

std::vector<Type*> Hx_order;

 feature jacobian, state jacobian, residual, order of state jacobian 을 선언해줌.

이는 Doc 에서 확인할 수 있으며, 다음과 같은 의미를 지님.

 

 

// Get the Jacobian for this feature

UpdaterHelper::get_feature_jacobian_full(state, feat, H_f, H_x, res, Hx_order);

H_f, H_x, res, Hx_order를 구해줌.

 

// Nullspace project

UpdaterHelper::nullspace_project_inplace(H_f, H_x, res);

 Docs 참고

 

/// Chi2 distance check

Eigen::MatrixXd P_marg = StateHelper::get_marginal_covariance(state, Hx_order);

Eigen::MatrixXd S = H_x*P_marg*H_x.transpose();

S.diagonal() += _options.sigma_pix_sq*Eigen::VectorXd::Ones(S.rows());

double chi2 = res.dot(S.llt().solve(res));

 chi2는 카이제곱 분포 관련 내용

 

// Get our threshold (we precompute up to 500 but handle the case that it is more)

double chi2_check;

if(res.rows() < 500) {

chi2_check = chi_squared_table[res.rows()];

} else {

boost::math::chi_squared chi_squared_dist(res.rows());

chi2_check = boost::math::quantile(chi_squared_dist, 0.95);

printf(YELLOW "chi2_check over the residual limit - %d\n" RESET, (int)res.rows());

}

 residual을 이용해 거리를 체크하는 듯, 오차가 심하면 에러발생.

 

// Check if we should delete or not

if(chi2 > _options.chi2_multipler*chi2_check) {

(*it2)->to_delete = true;

it2 = feature_vec.erase(it2);

//cout << "featid = " << feat.featid << endl;

//cout << "chi2 = " << chi2 << " > " << _options.chi2_multipler*chi2_check << endl;

//cout << "res = " << endl << res.transpose() << endl;

continue;

}

 삭제할지 말지 확인.

 

// We are good!!! Append to our large H vector

size_t ct_hx = 0;

for(const auto &var : Hx_order) {

// Ensure that this variable is in our Jacobian

if(Hx_mapping.find(var)==Hx_mapping.end()) {

Hx_mapping.insert({var,ct_jacob});

Hx_order_big.push_back(var);

ct_jacob += var->size();

}

// Append to our large Jacobian

Hx_big.block(ct_meas,Hx_mapping[var],H_x.rows(),var->size()) = H_x.block(0,ct_hx,H_x.rows(),var->size());

ct_hx += var->size();

}

 문제가 없으면 large H vector에 값들을 넣음.

 

// Append our residual and move forward

res_big.block(ct_meas,0,res.rows(),1) = res;

ct_meas += res.rows();

it2++;

 문제가 없으면 residual도 넣고 다음 feature에 대해 작업.

 

// We have appended all features to our Hx_big, res_big

// Delete it so we do not reuse information

for (size_t f=0; f < feature_vec.size(); f++) {

feature_vec[f]->to_delete = true;

}

 feature 데이터 삭제.

 

// Return if we don't have anything and resize our matrices

if(ct_meas < 1) {

return;

}

assert(ct_meas<=max_meas_size);

assert(ct_jacob<=max_hx_size);

res_big.conservativeResize(ct_meas,1);

Hx_big.conservativeResize(ct_meas,ct_jacob);

 작업할게 없으면 그냥 반환.

 

// 5. Perform measurement compression

UpdaterHelper::measurement_compress_inplace(Hx_big, res_big);

if(Hx_big.rows() < 1) {

return;

}

 update할 데이터가 너무 클 수 있으므로 압축을 통해 진행.

Docs 참고

 

// Our noise is isotropic, so make it here after our compression

Eigen::MatrixXd R_big = _options.sigma_pix_sq*Eigen::MatrixXd::Identity(res_big.rows(),res_big.rows());

 noise 추가.

 

// 6. With all good features update the state

StateHelper::EKFUpdate(state, Hx_order_big, Hx_big, res_big, R_big);

 드디어 업데이트 수행.

 

 

 

Feature::clean_old_measurements()

 파라미터에 해당하는 timestamps에서 발생하지 않은 measurements 들을 제거한다.

        /**
         * @brief Remove measurements that do not occur at passed timestamps.
         *
         * Given a series of valid timestamps, this will remove all measurements that have not occurred at these times.
         * This would normally be used to ensure that the measurements that we have occur at our clone times.
         *
         * @param valid_times Vector of timestamps that our measurements must occur at
         */
        void clean_old_measurements(std::vector<double> valid_times);


void Feature::clean_old_measurements(std::vector<double> valid_times) {


    // Loop through each of the cameras we have
    for(auto const &pair : timestamps) {

        // Assert that we have all the parts of a measurement
        assert(timestamps[pair.first].size() == uvs[pair.first].size());
        assert(timestamps[pair.first].size() == uvs_norm[pair.first].size());

        // Our iterators
        auto it1 = timestamps[pair.first].begin();
        auto it2 = uvs[pair.first].begin();
        auto it3 = uvs_norm[pair.first].begin();

        // Loop through measurement times, remove ones that are not in our timestamps
        while (it1 != timestamps[pair.first].end()) {
            if (std::find(valid_times.begin(),valid_times.end(),*it1) == valid_times.end()) {
                it1 = timestamps[pair.first].erase(it1);
                it2 = uvs[pair.first].erase(it2);
                it3 = uvs_norm[pair.first].erase(it3);
            } else {
                ++it1;
                ++it2;
                ++it3;
            }
        }
    }

}


        /// Timestamps of each UV measurement (mapped by camera ID)
        std::unordered_map<size_t, std::vector<double>> timestamps;


        /// UV coordinates that this feature has been seen from (mapped by camera ID)
        std::unordered_map<size_t, std::vector<Eigen::VectorXf>> uvs;
        
        
        /// UV normalized coordinates that this feature has been seen from (mapped by camera ID)
        std::unordered_map<size_t, std::vector<Eigen::VectorXf>> uvs_norm;

 

// Loop through each of the cameras we have

for(auto const &pair : timestamps) {

 모든 카메라에 대해 반복함. 우리는 하나만 갖고 있음.

// Assert that we have all the parts of a measurement

assert(timestamps[pair.first].size() == uvs[pair.first].size());

assert(timestamps[pair.first].size() == uvs_norm[pair.first].size());

 timestamps에는 feature의 시간이 저장되고,

uvs에는 feature의 좌표가 저장되고,

uvs_norm에는 feature의 normalize된 좌표가 저장된다.

 

세 개의 값은 모두 같은 사이즈를 가져야 한다.

 

// Our iterators

auto it1 = timestamps[pair.first].begin();

auto it2 = uvs[pair.first].begin();

auto it3 = uvs_norm[pair.first].begin();

 iterator를 받아온다.

// Loop through measurement times, remove ones that are not in our timestamps

while (it1 != timestamps[pair.first].end()) {

if (std::find(valid_times.begin(),valid_times.end(),*it1) == valid_times.end()) {

it1 = timestamps[pair.first].erase(it1);

it2 = uvs[pair.first].erase(it2);

it3 = uvs_norm[pair.first].erase(it3);

} else {

++it1;

++it2;

++it3;

}

}

 해당 timestamps에 해당하는 feature가 있는지 확인하고, 없다면 해당 timestamps, uvs, uvs_norm 모두 지워버린다.

 

 

 

 

 

FeatureInitializer::single_triangulation()

mono camera를 이용해 연속된 프레임을 대상으로 triangulation을 수행한다.

 

근데 내가 보기엔 depth 정보는 아직 감안하지 않은 것 같다.

 

Cipf는 camera pose에서 features 이고,

Apf는 Anchor frame에서 features 이고,

ApCi는 Anchor frame에서 camera pose이고,

CiAR은 Camera pose와 Anchor frame 간의 회전행렬이다.

 

즉, Camera pose에서 features를 얻기 위해서는 Anchor frame에서 features로부터 camera pose 에 대한 내용을 뺀 뒤 Camera pose와 Anchor frame에 대한 회전 행렬을 곱해주면 된다.

 

그리고 이를 정리하면 다음과 같은 수식을 얻을 수 있다.

 Anchor frame 에 대한 features 인 것이다.

노이즈가 없는 상태에서 camera pose에 대한 features인 Cipf는 다음과 같이 나타낼 수 있다.

이때, b는 feature의 좌표(undistorted normalized image coordinates)이고, z는 각 feature의 깊이 정보이다.

 이를 위 식에 대입하면 다음과 같은 식을 구할 수 있다.

 이 때, b에 회전행렬 R을 곱하면 다음과 같이 나타낼 수 있다.

이후에 depth z를 구할 필요가 없도록 b에 perpendicular한 vector를 구하게 된다.

이 때, 벡터 b를 b의 norm으로 나누어 구하게 되는데, norm의 정의는 square root of dot product 가 된다.

square root of the dot product

 perpendicular(수직)한 벡터는 다음과 같음 형태를 갖으며,

수직하기 때문에 벡터 b와 곱했을 때 0이 되게 된다.

 그리고 이를 5번째 수식과 곱하면 다음과 같아진다. 

벡터 b와 n을 곱하면 0이 되므로 식은 다음과 같아진다.

어우 머리야

 

일단 여기서는 "linear system that can give us an initial guess for the 3D position of our feature" 를 구하는 것이다.

 

그리고 Apf에는 [x,y,z] 값이 존재하는데, z 값이 깊이 값이 된다.

 

 

 

 

 

bool FeatureInitializer::single_triangulation(Feature* feat, std::unordered_map<size_t,std::unordered_map<double,ClonePose>> &clonesCAM) {


    // Total number of measurements
    // Also set the first measurement to be the anchor frame
    int total_meas = 0;
    size_t anchor_most_meas = 0;
    size_t most_meas = 0;
    for (auto const& pair : feat->timestamps) {
        total_meas += (int)pair.second.size();
        if(pair.second.size() > most_meas) {
            anchor_most_meas = pair.first;
            most_meas = pair.second.size();
        }
    }
    feat->anchor_cam_id = anchor_most_meas;
    feat->anchor_clone_timestamp = feat->timestamps.at(feat->anchor_cam_id).back();

    // Our linear system matrices
    Eigen::MatrixXd A = Eigen::MatrixXd::Zero(2*total_meas, 3);
    Eigen::MatrixXd b = Eigen::MatrixXd::Zero(2*total_meas, 1);

    // Location in the linear system matrices
    size_t c = 0;

    // Get the position of the anchor pose
    ClonePose anchorclone = clonesCAM.at(feat->anchor_cam_id).at(feat->anchor_clone_timestamp);
    Eigen::Matrix<double,3,3> &R_GtoA = anchorclone.Rot();
    Eigen::Matrix<double,3,1> &p_AinG = anchorclone.pos();

    // Loop through each camera for this feature
    for (auto const& pair : feat->timestamps) {

        // Add CAM_I features
        for (size_t m = 0; m < feat->timestamps.at(pair.first).size(); m++) {

            // Get the position of this clone in the global
            Eigen::Matrix<double, 3, 3> &R_GtoCi = clonesCAM.at(pair.first).at(feat->timestamps.at(pair.first).at(m)).Rot();
            Eigen::Matrix<double, 3, 1> &p_CiinG = clonesCAM.at(pair.first).at(feat->timestamps.at(pair.first).at(m)).pos();

            // Convert current position relative to anchor
            Eigen::Matrix<double,3,3> R_AtoCi;
            R_AtoCi.noalias() = R_GtoCi*R_GtoA.transpose();
            Eigen::Matrix<double,3,1> p_CiinA;
            p_CiinA.noalias() = R_GtoA*(p_CiinG-p_AinG);

            // Get the UV coordinate normal
            Eigen::Matrix<double, 3, 1> b_i;
            b_i << feat->uvs_norm.at(pair.first).at(m)(0), feat->uvs_norm.at(pair.first).at(m)(1), 1;
            b_i = R_AtoCi.transpose() * b_i;
            b_i = b_i / b_i.norm();
            Eigen::Matrix<double,2,3> Bperp = Eigen::Matrix<double,2,3>::Zero();
            Bperp << -b_i(2, 0), 0, b_i(0, 0), 0, b_i(2, 0), -b_i(1, 0);

            // Append to our linear system
            A.block(2 * c, 0, 2, 3) = Bperp;
            b.block(2 * c, 0, 2, 1).noalias() = Bperp * p_CiinA;
            c++;

        }
    }

    // Solve the linear system
    Eigen::MatrixXd p_f = A.colPivHouseholderQr().solve(b);

    // Check A and p_f
    Eigen::JacobiSVD<Eigen::MatrixXd> svd(A, Eigen::ComputeThinU | Eigen::ComputeThinV);
    Eigen::MatrixXd singularValues;
    singularValues.resize(svd.singularValues().rows(), 1);
    singularValues = svd.singularValues();
    double condA = singularValues(0, 0) / singularValues(singularValues.rows() - 1, 0);

    // If we have a bad condition number, or it is too close
    // Then set the flag for bad (i.e. set z-axis to nan)
    if (std::abs(condA) > _options.max_cond_number || p_f(2,0) < _options.min_dist || p_f(2,0) > _options.max_dist || std::isnan(p_f.norm())) {
        return false;
    }

    // Store it in our feature object
    feat->p_FinA = p_f;
    feat->p_FinG = R_GtoA.transpose()*feat->p_FinA + p_AinG;
    return true;

}

 

// Total number of measurements

// Also set the first measurement to be the anchor frame

int total_meas = 0;

size_t anchor_most_meas = 0;

size_t most_meas = 0;

for (auto const& pair : feat->timestamps) {

total_meas += (int)pair.second.size();

if(pair.second.size() > most_meas) {

anchor_most_meas = pair.first;

most_meas = pair.second.size();

}

}

feat->anchor_cam_id = anchor_most_meas;

feat->anchor_clone_timestamp = feat->timestamps.at(feat->anchor_cam_id).back();

우리는 mono camera를 사용하니 if 부분은 신경 안써도 되겠다.

features의 전체 크기를 구하고,

마지막 feature를 anchor frame으로 설정해준다. 

(왜 주석에서는 first measurement라고 했을까?)

 

// Our linear system matrices

Eigen::MatrixXd A = Eigen::MatrixXd::Zero(2*total_meas, 3);

Eigen::MatrixXd b = Eigen::MatrixXd::Zero(2*total_meas, 1);

흠 왜 이렇게 만들까

 

// Location in the linear system matrices

size_t c = 0;

 흠

 

// Get the position of the anchor pose

ClonePose anchorclone = clonesCAM.at(feat->anchor_cam_id).at(feat->anchor_clone_timestamp);

Eigen::Matrix<double,3,3> &R_GtoA = anchorclone.Rot();

Eigen::Matrix<double,3,1> &p_AinG = anchorclone.pos();

 이제 anchorclone의 값들을 가져온다.

 

// Loop through each camera for this feature

for (auto const& pair : feat->timestamps) {

각 카메라에 대한 반복문을 수행한다. 우리는 하나의 카메라만 사용한다.

 

// Add CAM_I features

for (size_t m = 0; m < feat->timestamps.at(pair.first).size(); m++) {

 해당 카메라의 features들에 대해 반복문을 수행한다.

 

// Get the position of this clone in the global

Eigen::Matrix<double, 3, 3> &R_GtoCi = clonesCAM.at(pair.first).at(feat->timestamps.at(pair.first).at(m)).Rot();

Eigen::Matrix<double, 3, 1> &p_CiinG = clonesCAM.at(pair.first).at(feat->timestamps.at(pair.first).at(m)).pos();

 각 feature에 대한 clonesCAM 들을 가져온다.

 

// Convert current position relative to anchor

Eigen::Matrix<double,3,3> R_AtoCi;

R_AtoCi.noalias() = R_GtoCi*R_GtoA.transpose();

Eigen::Matrix<double,3,1> p_CiinA;

p_CiinA.noalias() = R_GtoA*(p_CiinG-p_AinG);

 anchor cloneCAM 값과 각 features들의 cloneCAM 값을 곱해준다.

 

// Get the UV coordinate normal

Eigen::Matrix<double, 3, 1> b_i;

b_i << feat->uvs_norm.at(pair.first).at(m)(0), feat->uvs_norm.at(pair.first).at(m)(1), 1;

b_i = R_AtoCi.transpose() * b_i;

b_i = b_i / b_i.norm();

Eigen::Matrix<double,2,3> Bperp = Eigen::Matrix<double,2,3>::Zero();

Bperp << -b_i(2, 0), 0, b_i(0, 0), 0, b_i(2, 0), -b_i(1, 0);

// UV normalized coordinates that this feature has been seen from (mapped by camera ID)

std::unordered_map<size_t, std::vector<Eigen::VectorXf>> uvs_norm;

 

uvs_norm은 features의 좌표들이 저장되어 있다. 

이 좌표들에 R_AtoCi를 곱하게 되면 anchor_clone으로부터 회전된 features의 좌표들을 구할 수 있다.

 

다음 수식과 같다고 볼 수 있다.

 

 

b_i는 하나의 vector이다. 

이러한 벡터가 존재할 때, Eigen::norm() 연산은 square root of dot production 을 통해 벡터의 길이를 구할 수 있게 해준다.

square root of the dot product

그리고 해당 벡터를 벡터의 길이로 나눈 값은 vector b_i에 대해 perpendicular(수직)하게 된다.

즉, 다음 벡터들을 구한 것이다.

// Append to our linear system

A.block(2 * c, 0, 2, 3) = Bperp;

b.block(2 * c, 0, 2, 1).noalias() = Bperp * p_CiinA;

c++;

A는 위 수식의 [An1,An2]가 되고, b는 오른쪽 항이 된다.

 

// Solve the linear system

Eigen::MatrixXd p_f = A.colPivHouseholderQr().solve(b);

colPivHouseholderQr().solve()는 Ax=b 라는 행렬이 존재할 때, x를 구해서 반환해준다.

즉, 아래 수식에서 Apf를 구한 것이다.

// Check A and p_f

Eigen::JacobiSVD<Eigen::MatrixXd> svd(A, Eigen::ComputeThinU | Eigen::ComputeThinV);

Eigen::MatrixXd singularValues;

singularValues.resize(svd.singularValues().rows(), 1);

singularValues = svd.singularValues();

double condA = singularValues(0, 0) / singularValues(singularValues.rows() - 1, 0);

 체크를 한다는데, 자세한 내용은 아직 모르겠다.

 

// If we have a bad condition number, or it is too close

// Then set the flag for bad (i.e. set z-axis to nan)

if (std::abs(condA) > _options.max_cond_number || p_f(2,0) < _options.min_dist || p_f(2,0) > _options.max_dist || std::isnan(p_f.norm())) {

return false;

}

체크한다. (역시 아직 자세히는 모르겠다.)

 

// Store it in our feature object

feat->p_FinA = p_f;

feat->p_FinG = R_GtoA.transpose()*feat->p_FinA + p_AinG;

return true;

 Anchor frame에 대한 feature의 tranform 들을 저장한다.

해당 함수의 최종 목적은 이

p_FinA와 p_FinG를 구하는 것이었던 것이다.

 

그리고 p_FinA 는 Anchor frame에서 [x,y,z] 를 갖고 있는데, z 값이 깊이 값이 된다.

 

 

 

 

 

 

FeatureInitializer::single_gaussnewton()

 

        /**
         * @brief Uses a nonlinear triangulation to refine initial linear estimate of the feature
         * @param feat Pointer to feature
         * @param clonesCAM Map between camera ID to map of timestamp to camera pose estimate (rotation from global to camera, position of camera in global frame)
         * @return Returns false if it fails to be optimize (based on the thresholds)
         */
        bool single_gaussnewton(Feature* feat, std::unordered_map<size_t,std::unordered_map<double,ClonePose>> &clonesCAM);
        
        bool FeatureInitializer::single_gaussnewton(Feature* feat, std::unordered_map<size_t,std::unordered_map<double,ClonePose>> &clonesCAM) {

    //Get into inverse depth
    double rho = 1/feat->p_FinA(2);
    double alpha = feat->p_FinA(0)/feat->p_FinA(2);
    double beta = feat->p_FinA(1)/feat->p_FinA(2);

    // Optimization parameters
    double lam = _options.init_lamda;
    double eps = 10000;
    int runs = 0;

    // Variables used in the optimization
    bool recompute = true;
    Eigen::Matrix<double,3,3> Hess = Eigen::Matrix<double,3,3>::Zero();
    Eigen::Matrix<double,3,1> grad = Eigen::Matrix<double,3,1>::Zero();

    // Cost at the last iteration
    double cost_old = compute_error(clonesCAM,feat,alpha,beta,rho);

    // Get the position of the anchor pose
    Eigen::Matrix<double,3,3> &R_GtoA = clonesCAM.at(feat->anchor_cam_id).at(feat->anchor_clone_timestamp).Rot();
    Eigen::Matrix<double,3,1> &p_AinG = clonesCAM.at(feat->anchor_cam_id).at(feat->anchor_clone_timestamp).pos();

    // Loop till we have either
    // 1. Reached our max iteration count
    // 2. System is unstable
    // 3. System has converged
    while (runs < _options.max_runs && lam < _options.max_lamda && eps > _options.min_dx) {

        // Triggers a recomputation of jacobians/information/gradients
        if (recompute) {

            Hess.setZero();
            grad.setZero();

            double err = 0;

            // Loop through each camera for this feature
            for (auto const& pair : feat->timestamps) {

                // Add CAM_I features
                for (size_t m = 0; m < feat->timestamps.at(pair.first).size(); m++) {

                    //=====================================================================================
                    //=====================================================================================

                    // Get the position of this clone in the global
                    Eigen::Matrix<double, 3, 3> &R_GtoCi = clonesCAM.at(pair.first).at(feat->timestamps[pair.first].at(m)).Rot();
                    Eigen::Matrix<double, 3, 1> &p_CiinG = clonesCAM.at(pair.first).at(feat->timestamps[pair.first].at(m)).pos();
                    // Convert current position relative to anchor
                    Eigen::Matrix<double,3,3> R_AtoCi;
                    R_AtoCi.noalias() = R_GtoCi*R_GtoA.transpose();
                    Eigen::Matrix<double,3,1> p_CiinA;
                    p_CiinA.noalias() = R_GtoA*(p_CiinG-p_AinG);
                    Eigen::Matrix<double,3,1> p_AinCi;
                    p_AinCi.noalias() = -R_AtoCi*p_CiinA;

                    //=====================================================================================
                    //=====================================================================================

                    // Middle variables of the system
                    double hi1 = R_AtoCi(0, 0) * alpha + R_AtoCi(0, 1) * beta + R_AtoCi(0, 2) + rho * p_AinCi(0, 0);
                    double hi2 = R_AtoCi(1, 0) * alpha + R_AtoCi(1, 1) * beta + R_AtoCi(1, 2) + rho * p_AinCi(1, 0);
                    double hi3 = R_AtoCi(2, 0) * alpha + R_AtoCi(2, 1) * beta + R_AtoCi(2, 2) + rho * p_AinCi(2, 0);
                    // Calculate jacobian
                    double d_z1_d_alpha = (R_AtoCi(0, 0) * hi3 - hi1 * R_AtoCi(2, 0)) / (pow(hi3, 2));
                    double d_z1_d_beta = (R_AtoCi(0, 1) * hi3 - hi1 * R_AtoCi(2, 1)) / (pow(hi3, 2));
                    double d_z1_d_rho = (p_AinCi(0, 0) * hi3 - hi1 * p_AinCi(2, 0)) / (pow(hi3, 2));
                    double d_z2_d_alpha = (R_AtoCi(1, 0) * hi3 - hi2 * R_AtoCi(2, 0)) / (pow(hi3, 2));
                    double d_z2_d_beta = (R_AtoCi(1, 1) * hi3 - hi2 * R_AtoCi(2, 1)) / (pow(hi3, 2));
                    double d_z2_d_rho = (p_AinCi(1, 0) * hi3 - hi2 * p_AinCi(2, 0)) / (pow(hi3, 2));
                    Eigen::Matrix<double, 2, 3> H;
                    H << d_z1_d_alpha, d_z1_d_beta, d_z1_d_rho, d_z2_d_alpha, d_z2_d_beta, d_z2_d_rho;
                    // Calculate residual
                    Eigen::Matrix<float, 2, 1> z;
                    z << hi1 / hi3, hi2 / hi3;
                    Eigen::Matrix<float, 2, 1> res = feat->uvs_norm.at(pair.first).at(m) - z;

                    //=====================================================================================
                    //=====================================================================================

                    // Append to our summation variables
                    err += std::pow(res.norm(), 2);
                    grad.noalias() += H.transpose() * res.cast<double>();
                    Hess.noalias() += H.transpose() * H;
                }

            }

        }

        // Solve Levenberg iteration
        Eigen::Matrix<double,3,3> Hess_l = Hess;
        for (size_t r=0; r < (size_t)Hess.rows(); r++) {
            Hess_l(r,r) *= (1.0+lam);
        }

        Eigen::Matrix<double,3,1> dx = Hess_l.colPivHouseholderQr().solve(grad);
        //Eigen::Matrix<double,3,1> dx = (Hess+lam*Eigen::MatrixXd::Identity(Hess.rows(), Hess.rows())).colPivHouseholderQr().solve(grad);

        // Check if error has gone down
        double cost = compute_error(clonesCAM,feat,alpha+dx(0,0),beta+dx(1,0),rho+dx(2,0));

        // Debug print
        //cout << "run = " << runs << " | cost = " << dx.norm() << " | lamda = " << lam << " | depth = " << 1/rho << endl;

        // Check if converged
        if (cost <= cost_old && (cost_old-cost)/cost_old < _options.min_dcost) {
            alpha += dx(0, 0);
            beta += dx(1, 0);
            rho += dx(2, 0);
            eps = 0;
            break;
        }

        // If cost is lowered, accept step
        // Else inflate lambda (try to make more stable)
        if (cost <= cost_old) {
            recompute = true;
            cost_old = cost;
            alpha += dx(0, 0);
            beta += dx(1, 0);
            rho += dx(2, 0);
            runs++;
            lam = lam/_options.lam_mult;
            eps = dx.norm();
        } else {
            recompute = false;
            lam = lam*_options.lam_mult;
            continue;
        }
    }

    // Revert to standard, and set to all
    feat->p_FinA(0) = alpha/rho;
    feat->p_FinA(1) = beta/rho;
    feat->p_FinA(2) = 1/rho;

    // Get tangent plane to x_hat
    Eigen::HouseholderQR<Eigen::MatrixXd> qr(feat->p_FinA);
    Eigen::MatrixXd Q = qr.householderQ();

    // Max baseline we have between poses
    double base_line_max = 0.0;

    // Check maximum baseline
    // Loop through each camera for this feature
    for (auto const& pair : feat->timestamps) {
        // Loop through the other clones to see what the max baseline is
        for (size_t m = 0; m < feat->timestamps.at(pair.first).size(); m++) {
            // Get the position of this clone in the global
            Eigen::Matrix<double,3,1> &p_CiinG  = clonesCAM.at(pair.first).at(feat->timestamps.at(pair.first).at(m)).pos();
            // Convert current position relative to anchor
            Eigen::Matrix<double,3,1> p_CiinA = R_GtoA*(p_CiinG-p_AinG);
            // Dot product camera pose and nullspace
            double base_line = ((Q.block(0,1,3,2)).transpose() * p_CiinA).norm();
            if (base_line > base_line_max) base_line_max = base_line;
        }
    }

    // Check if this feature is bad or not
    // 1. If the feature is too close
    // 2. If the feature is invalid
    // 3. If the baseline ratio is large
    if(feat->p_FinA(2) < _options.min_dist
        || feat->p_FinA(2) > _options.max_dist
        || (feat->p_FinA.norm() / base_line_max) > _options.max_baseline
        || std::isnan(feat->p_FinA.norm())) {
        return false;
    }

    // Finally get position in global frame
    feat->p_FinG = R_GtoA.transpose()*feat->p_FinA + p_AinG;
    return true;

}

 

//Get into inverse depth

double rho = 1/feat->p_FinA(2);

double alpha = feat->p_FinA(0)/feat->p_FinA(2);

double beta = feat->p_FinA(1)/feat->p_FinA(2);

feat->p_FinA(0) 는 0,

feat->p_FinA(1) 는 1,

feat->p_FinA(2) 는 z이다.

 

rho = 1/z

alpha = x/z

beta = y/z

 

// Optimization parameters

double lam = _options.init_lamda;

double eps = 10000;

int runs = 0;

 parameter 값.

 

// Variables used in the optimization

bool recompute = true;

Eigen::Matrix<double,3,3> Hess = Eigen::Matrix<double,3,3>::Zero();

Eigen::Matrix<double,3,1> grad = Eigen::Matrix<double,3,1>::Zero();

 최적화에 사용할 변수

 

// Cost at the last iteration

double cost_old = compute_error(clonesCAM,feat,alpha,beta,rho);

comput_error() 함수를 통해 추정된 상태의 error를 측정한다.

 

// Get the position of the anchor pose

Eigen::Matrix<double,3,3> &R_GtoA = clonesCAM.at(feat->anchor_cam_id).at(feat->anchor_clone_timestamp).Rot();

Eigen::Matrix<double,3,1> &p_AinG = clonesCAM.at(feat->anchor_cam_id).at(feat->anchor_clone_timestamp).pos();

 anchor pose의 position을 가져온다.

 

// Loop till we have either

// 1. Reached our max iteration count

// 2. System is unstable

// 3. System has converged

while (runs < _options.max_runs && lam < _options.max_lamda && eps > _options.min_dx) {

 주석참고,

 

// Triggers a recomputation of jacobians/information/gradients

if (recompute) {

 주석참고,

 

Hess.setZero();

grad.setZero();

double err = 0;

 선언

 

// Loop through each camera for this feature

for (auto const& pair : feat->timestamps) {

// Add CAM_I features

for (size_t m = 0; m < feat->timestamps.at(pair.first).size(); m++) {

 반복문

 

// Get the position of this clone in the global

Eigen::Matrix<double, 3, 3> &R_GtoCi = clonesCAM.at(pair.first).at(feat->timestamps[pair.first].at(m)).Rot();

Eigen::Matrix<double, 3, 1> &p_CiinG = clonesCAM.at(pair.first).at(feat->timestamps[pair.first].at(m)).pos();

// Convert current position relative to anchor

Eigen::Matrix<double,3,3> R_AtoCi;

R_AtoCi.noalias() = R_GtoCi*R_GtoA.transpose();

Eigen::Matrix<double,3,1> p_CiinA;

p_CiinA.noalias() = R_GtoA*(p_CiinG-p_AinG);

Eigen::Matrix<double,3,1> p_AinCi;

p_AinCi.noalias() = -R_AtoCi*p_CiinA;

 이미 설명함.

 

// Middle variables of the system

double hi1 = R_AtoCi(0, 0) * alpha + R_AtoCi(0, 1) * beta + R_AtoCi(0, 2) + rho * p_AinCi(0, 0);

double hi2 = R_AtoCi(1, 0) * alpha + R_AtoCi(1, 1) * beta + R_AtoCi(1, 2) + rho * p_AinCi(1, 0);

double hi3 = R_AtoCi(2, 0) * alpha + R_AtoCi(2, 1) * beta + R_AtoCi(2, 2) + rho * p_AinCi(2, 0);

 이미 설명함.

 

// Calculate jacobian

double d_z1_d_alpha = (R_AtoCi(0, 0) * hi3 - hi1 * R_AtoCi(2, 0)) / (pow(hi3, 2));

double d_z1_d_beta = (R_AtoCi(0, 1) * hi3 - hi1 * R_AtoCi(2, 1)) / (pow(hi3, 2));

double d_z1_d_rho = (p_AinCi(0, 0) * hi3 - hi1 * p_AinCi(2, 0)) / (pow(hi3, 2));

double d_z2_d_alpha = (R_AtoCi(1, 0) * hi3 - hi2 * R_AtoCi(2, 0)) / (pow(hi3, 2));

double d_z2_d_beta = (R_AtoCi(1, 1) * hi3 - hi2 * R_AtoCi(2, 1)) / (pow(hi3, 2));

double d_z2_d_rho = (p_AinCi(1, 0) * hi3 - hi2 * p_AinCi(2, 0)) / (pow(hi3, 2));

Eigen::Matrix<double, 2, 3> H;

H << d_z1_d_alpha, d_z1_d_beta, d_z1_d_rho, d_z2_d_alpha, d_z2_d_beta, d_z2_d_rho;

 잘은 모르겠지만 해당 수식과 관계있는 듯. (Jacobian)

// Calculate residual

Eigen::Matrix<float, 2, 1> z;

z << hi1 / hi3, hi2 / hi3;

Eigen::Matrix<float, 2, 1> res = feat->uvs_norm.at(pair.first).at(m) - z;

// Append to our summation variables

err += std::pow(res.norm(), 2);

grad.noalias() += H.transpose() * res.cast<double>();

Hess.noalias() += H.transpose() * H;

 위 세 내용을 구함.

 

// Solve Levenberg iteration

Eigen::Matrix<double,3,3> Hess_l = Hess;

for (size_t r=0; r < (size_t)Hess.rows(); r++) {

Hess_l(r,r) *= (1.0+lam);

}

 Levenberg iteration. 추후에 확인하자.

 

Eigen::Matrix<double,3,1> dx = Hess_l.colPivHouseholderQr().solve(grad);

 solver. 

여기서 기존의 Apf가 새롭게 구해짐.

 

 

// Check if error has gone down

double cost = compute_error(clonesCAM,feat,alpha+dx(0,0),beta+dx(1,0),rho+dx(2,0));

 다시 error 체크

 

// Check if converged

if (cost <= cost_old && (cost_old-cost)/cost_old < _options.min_dcost) {

alpha += dx(0, 0);

beta += dx(1, 0);

rho += dx(2, 0);

eps = 0;

break;

}

 converged 되었는지 체크

 

// If cost is lowered, accept step

// Else inflate lambda (try to make more stable)

if (cost <= cost_old) {

recompute = true;

cost_old = cost;

alpha += dx(0, 0);

beta += dx(1, 0);

rho += dx(2, 0);

runs++;

lam = lam/_options.lam_mult;

eps = dx.norm();

} else {

recompute = false;

lam = lam*_options.lam_mult;

continue;

}

 cost의 값에 따라 파라미터 값을 조정.

 

// Revert to standard, and set to all

feat->p_FinA(0) = alpha/rho;

feat->p_FinA(1) = beta/rho;

feat->p_FinA(2) = 1/rho;

 resetting

 

// Get tangent plane to x_hat

Eigen::HouseholderQR<Eigen::MatrixXd> qr(feat->p_FinA);

Eigen::MatrixXd Q = qr.householderQ();

 QR decomposition으로부터 tangent plane 을 구해줌.

 

// Max baseline we have between poses

double base_line_max = 0.0;

 base line 선언

 

// Check maximum baseline

// Loop through each camera for this feature

for (auto const& pair : feat->timestamps) {

// Loop through the other clones to see what the max baseline is

for (size_t m = 0; m < feat->timestamps.at(pair.first).size(); m++) {

// Get the position of this clone in the global

Eigen::Matrix<double,3,1> &p_CiinG = clonesCAM.at(pair.first).at(feat->timestamps.at(pair.first).at(m)).pos();

// Convert current position relative to anchor

Eigen::Matrix<double,3,1> p_CiinA = R_GtoA*(p_CiinG-p_AinG);

// Dot product camera pose and nullspace

double base_line = ((Q.block(0,1,3,2)).transpose() * p_CiinA).norm();

if (base_line > base_line_max) base_line_max = base_line;

}

}

 maximum baseline을 구해줌.

 

// Check if this feature is bad or not

// 1. If the feature is too close

// 2. If the feature is invalid

// 3. If the baseline ratio is large

if(feat->p_FinA(2) < _options.min_dist

|| feat->p_FinA(2) > _options.max_dist

|| (feat->p_FinA.norm() / base_line_max) > _options.max_baseline

|| std::isnan(feat->p_FinA.norm())) {

return false;

}

 불량체크

 

// Finally get position in global frame

feat->p_FinG = R_GtoA.transpose()*feat->p_FinA + p_AinG;

return true;

 최종적으로 global frame에서의 position이 구해짐.

 

 

 

 

FeatureInitializer::compute_error()

 

        /**
         * @brief Helper function for the gauss newton method that computes error of the given estimate
         * @param clonesCAM Map between camera ID to map of timestamp to camera pose estimate
         * @param feat Pointer to the feature
         * @param alpha x/z in anchor
         * @param beta y/z in anchor
         * @param rho 1/z inverse depth
         */
        double compute_error(std::unordered_map<size_t,std::unordered_map<double,ClonePose>> &clonesCAM,Feature* feat,double alpha,double beta,double rho);

double FeatureInitializer::compute_error(std::unordered_map<size_t,std::unordered_map<double,ClonePose>> &clonesCAM,
                                         Feature* feat, double alpha, double beta, double rho) {

    // Total error
    double err = 0;

    // Get the position of the anchor pose
    Eigen::Matrix<double,3,3> &R_GtoA = clonesCAM.at(feat->anchor_cam_id).at(feat->anchor_clone_timestamp).Rot();
    Eigen::Matrix<double,3,1> &p_AinG = clonesCAM.at(feat->anchor_cam_id).at(feat->anchor_clone_timestamp).pos();

    // Loop through each camera for this feature
    for (auto const& pair : feat->timestamps) {
        // Add CAM_I features
        for (size_t m = 0; m < feat->timestamps.at(pair.first).size(); m++) {

            //=====================================================================================
            //=====================================================================================

            // Get the position of this clone in the global
            Eigen::Matrix<double, 3, 3> &R_GtoCi = clonesCAM.at(pair.first).at(feat->timestamps.at(pair.first).at(m)).Rot();
            Eigen::Matrix<double, 3, 1> &p_CiinG = clonesCAM.at(pair.first).at(feat->timestamps.at(pair.first).at(m)).pos();
            // Convert current position relative to anchor
            Eigen::Matrix<double,3,3> R_AtoCi;
            R_AtoCi.noalias() = R_GtoCi*R_GtoA.transpose();
            Eigen::Matrix<double,3,1> p_CiinA;
            p_CiinA.noalias() = R_GtoA*(p_CiinG-p_AinG);
            Eigen::Matrix<double,3,1> p_AinCi;
            p_AinCi.noalias() = -R_AtoCi*p_CiinA;

            //=====================================================================================
            //=====================================================================================

            // Middle variables of the system
            double hi1 = R_AtoCi(0, 0) * alpha + R_AtoCi(0, 1) * beta + R_AtoCi(0, 2) + rho * p_AinCi(0, 0);
            double hi2 = R_AtoCi(1, 0) * alpha + R_AtoCi(1, 1) * beta + R_AtoCi(1, 2) + rho * p_AinCi(1, 0);
            double hi3 = R_AtoCi(2, 0) * alpha + R_AtoCi(2, 1) * beta + R_AtoCi(2, 2) + rho * p_AinCi(2, 0);
            // Calculate residual
            Eigen::Matrix<float, 2, 1> z;
            z << hi1 / hi3, hi2 / hi3;
            Eigen::Matrix<float, 2, 1> res = feat->uvs_norm.at(pair.first).at(m) - z;
            // Append to our summation variables
            err += pow(res.norm(), 2);
        }
    }

    return err;

}

 

// Total error

double err = 0;

 error 선언 및 초기화

 

// Get the position of the anchor pose

Eigen::Matrix<double,3,3> &R_GtoA = clonesCAM.at(feat->anchor_cam_id).at(feat->anchor_clone_timestamp).Rot();

Eigen::Matrix<double,3,1> &p_AinG = clonesCAM.at(feat->anchor_cam_id).at(feat->anchor_clone_timestamp).pos();

 anchor pose 의 position 을 가져옴.

 

// Loop through each camera for this feature

for (auto const& pair : feat->timestamps) {

// Add CAM_I features

for (size_t m = 0; m < feat->timestamps.at(pair.first).size(); m++) {

 feature 반복문

 

// Get the position of this clone in the global

Eigen::Matrix<double, 3, 3> &R_GtoCi = clonesCAM.at(pair.first).at(feat->timestamps.at(pair.first).at(m)).Rot();

Eigen::Matrix<double, 3, 1> &p_CiinG = clonesCAM.at(pair.first).at(feat->timestamps.at(pair.first).at(m)).pos();

 해당 clone의 global position을 가져옴

 

// Convert current position relative to anchor

Eigen::Matrix<double,3,3> R_AtoCi;

R_AtoCi.noalias() = R_GtoCi*R_GtoA.transpose();

Eigen::Matrix<double,3,1> p_CiinA;

p_CiinA.noalias() = R_GtoA*(p_CiinG-p_AinG);

Eigen::Matrix<double,3,1> p_AinCi;

p_AinCi.noalias() = -R_AtoCi*p_CiinA;

 Anchor와 관련하여 position을 수정해줌.

 

// Middle variables of the system

double hi1 = R_AtoCi(0, 0) * alpha + R_AtoCi(0, 1) * beta + R_AtoCi(0, 2) + rho * p_AinCi(0, 0);

double hi2 = R_AtoCi(1, 0) * alpha + R_AtoCi(1, 1) * beta + R_AtoCi(1, 2) + rho * p_AinCi(1, 0);

double hi3 = R_AtoCi(2, 0) * alpha + R_AtoCi(2, 1) * beta + R_AtoCi(2, 2) + rho * p_AinCi(2, 0);

 system의 middle variables을 구해줌. 참고

Measurement Update Derivations » 3D Feature Triangulation | OpenVINS

// Calculate residual

Eigen::Matrix<float, 2, 1> z;

z << hi1 / hi3, hi2 / hi3;

Eigen::Matrix<float, 2, 1> res = feat->uvs_norm.at(pair.first).at(m) - z;

 residual을 계산함.

 

// Append to our summation variables

err += pow(res.norm(), 2);

 

return err;

 error를 반환한다.

 

 

 

UpdaterHelper::get_feature_jacobian_full()

        /**
         * @brief Will construct the "stacked" Jacobians for a single feature from all its measurements
         *
         * @param[in] state State of the filter system
         * @param[in] feature Feature we want to get Jacobians of (must have feature means)
         * @param[out] H_f Jacobians in respect to the feature error state
         * @param[out] H_x Extra Jacobians in respect to the state (for example anchored pose)
         * @param[out] res Measurement residual for this feature
         * @param[out] x_order Extra variables our extra Jacobian has (for example anchored pose)
         */
        static void get_feature_jacobian_full(State* state, UpdaterHelperFeature &feature, Eigen::MatrixXd &H_f, Eigen::MatrixXd &H_x, Eigen::VectorXd &res, std::vector<Type*> &x_order);

void UpdaterHelper::get_feature_jacobian_full(State* state, UpdaterHelperFeature &feature, Eigen::MatrixXd &H_f, Eigen::MatrixXd &H_x, Eigen::VectorXd &res, std::vector<Type*> &x_order) {

    // Total number of measurements for this feature
    int total_meas = 0;
    for (auto const& pair : feature.timestamps) {
        total_meas += (int)pair.second.size();
    }

    // Compute the size of the states involved with this feature
    int total_hx = 0;
    std::unordered_map<Type*,size_t> map_hx;
    for (auto const& pair : feature.timestamps) {

        // Our extrinsics and intrinsics
        PoseJPL *calibration = state->_calib_IMUtoCAM.at(pair.first);
        Vec *distortion = state->_cam_intrinsics.at(pair.first);

        // If doing calibration extrinsics
        if(state->_options.do_calib_camera_pose) {
            map_hx.insert({calibration,total_hx});
            x_order.push_back(calibration);
            total_hx += calibration->size();
        }

        // If doing calibration intrinsics
        if(state->_options.do_calib_camera_intrinsics) {
            map_hx.insert({distortion,total_hx});
            x_order.push_back(distortion);
            total_hx += distortion->size();
        }

        // Loop through all measurements for this specific camera
        for (size_t m = 0; m < feature.timestamps[pair.first].size(); m++) {

            // Add this clone if it is not added already
            PoseJPL *clone_Ci = state->_clones_IMU.at(feature.timestamps[pair.first].at(m));
            if(map_hx.find(clone_Ci) == map_hx.end()) {
                map_hx.insert({clone_Ci,total_hx});
                x_order.push_back(clone_Ci);
                total_hx += clone_Ci->size();
            }

        }

    }

    // If we are using an anchored representation, make sure that the anchor is also added
    if (LandmarkRepresentation::is_relative_representation(feature.feat_representation)) {

        // Assert we have a clone
        assert(feature.anchor_cam_id != -1);

        // Add this anchor if it is not added already
        PoseJPL *clone_Ai = state->_clones_IMU.at(feature.anchor_clone_timestamp);
        if(map_hx.find(clone_Ai) == map_hx.end()) {
            map_hx.insert({clone_Ai,total_hx});
            x_order.push_back(clone_Ai);
            total_hx += clone_Ai->size();
        }

        // Also add its calibration if we are doing calibration
        if(state->_options.do_calib_camera_pose) {
            // Add this anchor if it is not added already
            PoseJPL *clone_calib = state->_calib_IMUtoCAM.at(feature.anchor_cam_id);
            if(map_hx.find(clone_calib) == map_hx.end()) {
                map_hx.insert({clone_calib,total_hx});
                x_order.push_back(clone_calib);
                total_hx += clone_calib->size();
            }
        }

    }

    //=========================================================================
    //=========================================================================

    // Calculate the position of this feature in the global frame
    // If anchored, then we need to calculate the position of the feature in the global
    Eigen::Vector3d p_FinG = feature.p_FinG;
    if(LandmarkRepresentation::is_relative_representation(feature.feat_representation)) {
        // Assert that we have an anchor pose for this feature
        assert(feature.anchor_cam_id!=-1);
        // Get calibration for our anchor camera
        Eigen::Matrix<double, 3, 3> R_ItoC = state->_calib_IMUtoCAM.at(feature.anchor_cam_id)->Rot();
        Eigen::Matrix<double, 3, 1> p_IinC = state->_calib_IMUtoCAM.at(feature.anchor_cam_id)->pos();
        // Anchor pose orientation and position
        Eigen::Matrix<double,3,3> R_GtoI = state->_clones_IMU.at(feature.anchor_clone_timestamp)->Rot();
        Eigen::Matrix<double,3,1> p_IinG = state->_clones_IMU.at(feature.anchor_clone_timestamp)->pos();
        // Feature in the global frame
        p_FinG = R_GtoI.transpose() * R_ItoC.transpose()*(feature.p_FinA - p_IinC) + p_IinG;
    }

    // Calculate the position of this feature in the global frame FEJ
    // If anchored, then we can use the "best" p_FinG since the value of p_FinA does not matter
    Eigen::Vector3d p_FinG_fej = feature.p_FinG_fej;
    if(LandmarkRepresentation::is_relative_representation(feature.feat_representation)) {
        p_FinG_fej = p_FinG;
    }

    //=========================================================================
    //=========================================================================

    // Allocate our residual and Jacobians
    int c = 0;
    int jacobsize = (feature.feat_representation!=LandmarkRepresentation::Representation::ANCHORED_INVERSE_DEPTH_SINGLE) ? 3 : 1;
    res = Eigen::VectorXd::Zero(2*total_meas);
    H_f = Eigen::MatrixXd::Zero(2*total_meas,jacobsize);
    H_x = Eigen::MatrixXd::Zero(2*total_meas,total_hx);

    // Derivative of p_FinG in respect to feature representation.
    // This only needs to be computed once and thus we pull it out of the loop
    Eigen::MatrixXd dpfg_dlambda;
    std::vector<Eigen::MatrixXd> dpfg_dx;
    std::vector<Type*> dpfg_dx_order;
    UpdaterHelper::get_feature_jacobian_representation(state, feature, dpfg_dlambda, dpfg_dx, dpfg_dx_order);

    // Assert that all the ones in our order are already in our local jacobian mapping
    for(auto &type : dpfg_dx_order) {
        assert(map_hx.find(type)!=map_hx.end());
    }

    // Loop through each camera for this feature
    for (auto const& pair : feature.timestamps) {

        // Our calibration between the IMU and CAMi frames
        Vec* distortion = state->_cam_intrinsics.at(pair.first);
        PoseJPL* calibration = state->_calib_IMUtoCAM.at(pair.first);
        Eigen::Matrix<double,3,3> R_ItoC = calibration->Rot();
        Eigen::Matrix<double,3,1> p_IinC = calibration->pos();
        Eigen::Matrix<double,8,1> cam_d = distortion->value();

        // Loop through all measurements for this specific camera
        for (size_t m = 0; m < feature.timestamps[pair.first].size(); m++) {

            //=========================================================================
            //=========================================================================

            // Get current IMU clone state
            PoseJPL* clone_Ii = state->_clones_IMU.at(feature.timestamps[pair.first].at(m));
            Eigen::Matrix<double,3,3> R_GtoIi = clone_Ii->Rot();
            Eigen::Matrix<double,3,1> p_IiinG = clone_Ii->pos();

            // Get current feature in the IMU
            Eigen::Matrix<double,3,1> p_FinIi = R_GtoIi*(p_FinG-p_IiinG);

            // Project the current feature into the current frame of reference
            Eigen::Matrix<double,3,1> p_FinCi = R_ItoC*p_FinIi+p_IinC;
            Eigen::Matrix<double,2,1> uv_norm;
            uv_norm << p_FinCi(0)/p_FinCi(2),p_FinCi(1)/p_FinCi(2);

            // Distort the normalized coordinates (false=radtan, true=fisheye)
            Eigen::Matrix<double,2,1> uv_dist;

            // Calculate distortion uv and jacobian
            if(state->_cam_intrinsics_model.at(pair.first)) {

                // Calculate distorted coordinates for fisheye
                double r = std::sqrt(uv_norm(0)*uv_norm(0)+uv_norm(1)*uv_norm(1));
                double theta = std::atan(r);
                double theta_d = theta+cam_d(4)*std::pow(theta,3)+cam_d(5)*std::pow(theta,5)+cam_d(6)*std::pow(theta,7)+cam_d(7)*std::pow(theta,9);

                // Handle when r is small (meaning our xy is near the camera center)
                double inv_r = (r > 1e-8)? 1.0/r : 1.0;
                double cdist = (r > 1e-8)? theta_d * inv_r : 1.0;

                // Calculate distorted coordinates for fisheye
                double x1 = uv_norm(0)*cdist;
                double y1 = uv_norm(1)*cdist;
                uv_dist(0) = cam_d(0)*x1 + cam_d(2);
                uv_dist(1) = cam_d(1)*y1 + cam_d(3);

            } else {

                // Calculate distorted coordinates for radial
                double r = std::sqrt(uv_norm(0)*uv_norm(0)+uv_norm(1)*uv_norm(1));
                double r_2 = r*r;
                double r_4 = r_2*r_2;
                double x1 = uv_norm(0)*(1+cam_d(4)*r_2+cam_d(5)*r_4)+2*cam_d(6)*uv_norm(0)*uv_norm(1)+cam_d(7)*(r_2+2*uv_norm(0)*uv_norm(0));
                double y1 = uv_norm(1)*(1+cam_d(4)*r_2+cam_d(5)*r_4)+cam_d(6)*(r_2+2*uv_norm(1)*uv_norm(1))+2*cam_d(7)*uv_norm(0)*uv_norm(1);
                uv_dist(0) = cam_d(0)*x1 + cam_d(2);
                uv_dist(1) = cam_d(1)*y1 + cam_d(3);

            }

            // Our residual
            Eigen::Matrix<double,2,1> uv_m;
            uv_m << (double)feature.uvs[pair.first].at(m)(0), (double)feature.uvs[pair.first].at(m)(1);
            res.block(2*c,0,2,1) = uv_m - uv_dist;


            //=========================================================================
            //=========================================================================

            // If we are doing first estimate Jacobians, then overwrite with the first estimates
            if(state->_options.do_fej) {
                R_GtoIi = clone_Ii->Rot_fej();
                p_IiinG = clone_Ii->pos_fej();
                //R_ItoC = calibration->Rot_fej();
                //p_IinC = calibration->pos_fej();
                p_FinIi = R_GtoIi*(p_FinG_fej-p_IiinG);
                p_FinCi = R_ItoC*p_FinIi+p_IinC;
                //uv_norm << p_FinCi(0)/p_FinCi(2),p_FinCi(1)/p_FinCi(2);
                //cam_d = state->get_intrinsics_CAM(pair.first)->fej();
            }

            // Compute Jacobians in respect to normalized image coordinates and possibly the camera intrinsics
            Eigen::Matrix<double,2,2> dz_dzn = Eigen::Matrix<double,2,2>::Zero();
            Eigen::Matrix<double,2,8> dz_dzeta = Eigen::Matrix<double,2,8>::Zero();
            UpdaterHelper::get_feature_jacobian_intrinsics(state, uv_norm, state->_cam_intrinsics_model.at(pair.first), cam_d, dz_dzn, dz_dzeta);

            // Normalized coordinates in respect to projection function
            Eigen::Matrix<double,2,3> dzn_dpfc = Eigen::Matrix<double,2,3>::Zero();
            dzn_dpfc << 1/p_FinCi(2),0,-p_FinCi(0)/(p_FinCi(2)*p_FinCi(2)),
                    0, 1/p_FinCi(2),-p_FinCi(1)/(p_FinCi(2)*p_FinCi(2));

            // Derivative of p_FinCi in respect to p_FinIi
            Eigen::Matrix<double,3,3> dpfc_dpfg = R_ItoC*R_GtoIi;

            // Derivative of p_FinCi in respect to camera clone state
            Eigen::Matrix<double,3,6> dpfc_dclone = Eigen::Matrix<double,3,6>::Zero();
            dpfc_dclone.block(0,0,3,3).noalias() = R_ItoC*skew_x(p_FinIi);
            dpfc_dclone.block(0,3,3,3) = -dpfc_dpfg;

            //=========================================================================
            //=========================================================================


            // Precompute some matrices
            Eigen::Matrix<double,2,3> dz_dpfc = dz_dzn*dzn_dpfc;
            Eigen::Matrix<double,2,3> dz_dpfg = dz_dpfc*dpfc_dpfg;

            // CHAINRULE: get the total feature Jacobian
            H_f.block(2*c,0,2,H_f.cols()).noalias() = dz_dpfg*dpfg_dlambda;

            // CHAINRULE: get state clone Jacobian
            H_x.block(2*c,map_hx[clone_Ii],2,clone_Ii->size()).noalias() = dz_dpfc*dpfc_dclone;

            // CHAINRULE: loop through all extra states and add their
            // NOTE: we add the Jacobian here as we might be in the anchoring pose for this measurement
            for(size_t i=0; i<dpfg_dx_order.size(); i++) {
                H_x.block(2*c,map_hx[dpfg_dx_order.at(i)],2,dpfg_dx_order.at(i)->size()).noalias() += dz_dpfg*dpfg_dx.at(i);
            }


            //=========================================================================
            //=========================================================================


            // Derivative of p_FinCi in respect to camera calibration (R_ItoC, p_IinC)
            if(state->_options.do_calib_camera_pose) {

                // Calculate the Jacobian
                Eigen::Matrix<double,3,6> dpfc_dcalib = Eigen::Matrix<double,3,6>::Zero();
                dpfc_dcalib.block(0,0,3,3) = skew_x(p_FinCi-p_IinC);
                dpfc_dcalib.block(0,3,3,3) = Eigen::Matrix<double,3,3>::Identity();

                // Chainrule it and add it to the big jacobian
                H_x.block(2*c,map_hx[calibration],2,calibration->size()).noalias() += dz_dpfc*dpfc_dcalib;

            }

            // Derivative of measurement in respect to distortion parameters
            if(state->_options.do_calib_camera_intrinsics) {
                H_x.block(2*c,map_hx[distortion],2,distortion->size()) = dz_dzeta;
            }

            // Move the Jacobian and residual index forward
            c++;

        }

    }


}

// Total number of measurements for this feature

int total_meas = 0;

for (auto const& pair : feature.timestamps) {

total_meas += (int)pair.second.size();

}

timestamps의 원형은 다음과 같다.

/// Timestamps of each UV measurement (mapped by camera ID)

std::unordered_map<size_t, std::vector<double>> timestamps;

 

그러므로 feature.timestamps 를 반복문으로 돌린다는 것은 

unordered_map 을 대상으로 돌린다는 것이고,

stereo camera의 경우에는 2번 돌리겠지만,

mono camera의 경우에는 1번만 돌아갈 것이다.

 

size_t에는 camera ID가 들어가고 std::vector<double> 에는 time 들이 vector 형으로 기록되게 된다. 

 

이러한 timestamps 의 주소를 pair 로 가져오게 되는 것이고, 

pair.first 는 camera ID 가 되는 것이다. 

 

pair.second.size()는 몇 개의 timestamp 데이터가 존재하는지를 구하는 것이다.

 

// Compute the size of the states involved with this feature

int total_hx = 0;

std::unordered_map<Type*,size_t> map_hx;

for (auto const& pair : feature.timestamps) {

 이제 해당하는 feature에 관련된 state의 개수를 구한다.

 

// Our extrinsics and intrinsics

PoseJPL *calibration = state->_calib_IMUtoCAM.at(pair.first);

Vec *distortion = state->_cam_intrinsics.at(pair.first);

 camera extrinsics 과 intrinsics을 가져온다.

 

// If doing calibration extrinsics

if(state->_options.do_calib_camera_pose) {

map_hx.insert({calibration,total_hx});

x_order.push_back(calibration);

total_hx += calibration->size();

}

// If doing calibration intrinsics

if(state->_options.do_calib_camera_intrinsics) {

map_hx.insert({distortion,total_hx});

x_order.push_back(distortion);

total_hx += distortion->size();

}

calibration을 하는 경우 수행한다.

 

// Loop through all measurements for this specific camera

for (size_t m = 0; m < feature.timestamps[pair.first].size(); m++) {

// Add this clone if it is not added already

PoseJPL *clone_Ci = state->_clones_IMU.at(feature.timestamps[pair.first].at(m));

if(map_hx.find(clone_Ci) == map_hx.end()) {

map_hx.insert({clone_Ci,total_hx});

x_order.push_back(clone_Ci);

total_hx += clone_Ci->size();

}

}

 

해당 feature에 대한 _clones_IMU 값을 가져온다.

 

calibration을 위한 값들도 조정해준다.

 

// If we are using an anchored representation, make sure that the anchor is also added

if (LandmarkRepresentation::is_relative_representation(feature.feat_representation)) {

// Assert we have a clone

assert(feature.anchor_cam_id != -1);

// Add this anchor if it is not added already

PoseJPL *clone_Ai = state->_clones_IMU.at(feature.anchor_clone_timestamp);

if(map_hx.find(clone_Ai) == map_hx.end()) {

map_hx.insert({clone_Ai,total_hx});

x_order.push_back(clone_Ai);

total_hx += clone_Ai->size();

}

// Also add its calibration if we are doing calibration

if(state->_options.do_calib_camera_pose) {

// Add this anchor if it is not added already

PoseJPL *clone_calib = state->_calib_IMUtoCAM.at(feature.anchor_cam_id);

if(map_hx.find(clone_calib) == map_hx.end()) {

map_hx.insert({clone_calib,total_hx});

x_order.push_back(clone_calib);

total_hx += clone_calib->size();

}

}

}

 우리는 GLOBAL_3D를 사용하므로 패스한다.

 

// Calculate the position of this feature in the global frame

// If anchored, then we need to calculate the position of the feature in the global

Eigen::Vector3d p_FinG = feature.p_FinG;

if(LandmarkRepresentation::is_relative_representation(feature.feat_representation)) {

// Assert that we have an anchor pose for this feature

assert(feature.anchor_cam_id!=-1);

// Get calibration for our anchor camera

Eigen::Matrix<double, 3, 3> R_ItoC = state->_calib_IMUtoCAM.at(feature.anchor_cam_id)->Rot();

Eigen::Matrix<double, 3, 1> p_IinC = state->_calib_IMUtoCAM.at(feature.anchor_cam_id)->pos();

// Anchor pose orientation and position

Eigen::Matrix<double,3,3> R_GtoI = state->_clones_IMU.at(feature.anchor_clone_timestamp)->Rot();

Eigen::Matrix<double,3,1> p_IinG = state->_clones_IMU.at(feature.anchor_clone_timestamp)->pos();

// Feature in the global frame

p_FinG = R_GtoI.transpose() * R_ItoC.transpose()*(feature.p_FinA - p_IinC) + p_IinG;

}

// Calculate the position of this feature in the global frame FEJ

// If anchored, then we can use the "best" p_FinG since the value of p_FinA does not matter

Eigen::Vector3d p_FinG_fej = feature.p_FinG_fej;

if(LandmarkRepresentation::is_relative_representation(feature.feat_representation)) {

p_FinG_fej = p_FinG;

}

 우리는 GLOBAL_3D를 사용하므로 두 가지만 신경쓰면 된다.

 

Eigen::Vector3d p_FinG = feature.p_FinG;

 

Eigen::Vector3d p_FinG_fej = feature.p_FinG_fej;

 

해당 feature의 Ground에서 위치정보를 가져온다.

 

// Allocate our residual and Jacobians

int c = 0;

int jacobsize = (feature.feat_representation!=LandmarkRepresentation::Representation::ANCHORED_INVERSE_DEPTH_SINGLE) ? 3 : 1;

res = Eigen::VectorXd::Zero(2*total_meas);

H_f = Eigen::MatrixXd::Zero(2*total_meas,jacobsize);

H_x = Eigen::MatrixXd::Zero(2*total_meas,total_hx);

 우리는 GLOBAL_3D를 사용하므로 jacobsize는 3이 될 것이다.

나머지는 다음과 같다.

 

 

// Derivative of p_FinG in respect to feature representation.

// This only needs to be computed once and thus we pull it out of the loop

Eigen::MatrixXd dpfg_dlambda;

std::vector<Eigen::MatrixXd> dpfg_dx;

std::vector<Type*> dpfg_dx_order;

UpdaterHelper::get_feature_jacobian_representation(state, feature, dpfg_dlambda, dpfg_dx, dpfg_dx_order);

 이제 representation type에 따라서 feature jacobian representation을 업데이트하게 되는데,

H_f 와 H_x 와 x_order 를 구하게 된다.

 

// Assert that all the ones in our order are already in our local jacobian mapping

for(auto &type : dpfg_dx_order) {

assert(map_hx.find(type)!=map_hx.end());

}

 

우리가 이미 구한 local jacobian mapping와 이번에 구한 jacobian이 같다면 예외처리를 한다.

 

// Loop through each camera for this feature

for (auto const& pair : feature.timestamps) {

 features 반복문

 

// Our calibration between the IMU and CAMi frames

Vec* distortion = state->_cam_intrinsics.at(pair.first);

PoseJPL* calibration = state->_calib_IMUtoCAM.at(pair.first);

Eigen::Matrix<double,3,3> R_ItoC = calibration->Rot();

Eigen::Matrix<double,3,1> p_IinC = calibration->pos();

Eigen::Matrix<double,8,1> cam_d = distortion->value();

 calibration 정보를 가져온다.

 

// Loop through all measurements for this specific camera

for (size_t m = 0; m < feature.timestamps[pair.first].size(); m++) {

해당 카메라에 대한 반복문을 수행한다.

 

// Get current IMU clone state

PoseJPL* clone_Ii = state->_clones_IMU.at(feature.timestamps[pair.first].at(m));

Eigen::Matrix<double,3,3> R_GtoIi = clone_Ii->Rot();

Eigen::Matrix<double,3,1> p_IiinG = clone_Ii->pos();

 해당 feature에 해당하는 _IMU_clone을 가져온다.

 

// Get current feature in the IMU

Eigen::Matrix<double,3,1> p_FinIi = R_GtoIi*(p_FinG-p_IiinG);

 imu에 대한 feature의 pose를 구해준다.

 

// Project the current feature into the current frame of reference

Eigen::Matrix<double,3,1> p_FinCi = R_ItoC*p_FinIi+p_IinC;

Eigen::Matrix<double,2,1> uv_norm;

uv_norm << p_FinCi(0)/p_FinCi(2),p_FinCi(1)/p_FinCi(2);

현재 feature를 현재 frame에 맞춰 사영한다. 

 

// Distort the normalized coordinates (false=radtan, true=fisheye)

Eigen::Matrix<double,2,1> uv_dist;

// Calculate distortion uv and jacobian

if(state->_cam_intrinsics_model.at(pair.first)) {

// Calculate distorted coordinates for fisheye

double r = std::sqrt(uv_norm(0)*uv_norm(0)+uv_norm(1)*uv_norm(1));

double theta = std::atan(r);

double theta_d = theta+cam_d(4)*std::pow(theta,3)+cam_d(5)*std::pow(theta,5)+cam_d(6)*std::pow(theta,7)+cam_d(7)*std::pow(theta,9);

// Handle when r is small (meaning our xy is near the camera center)

double inv_r = (r > 1e-8)? 1.0/r : 1.0;

double cdist = (r > 1e-8)? theta_d * inv_r : 1.0;

// Calculate distorted coordinates for fisheye

double x1 = uv_norm(0)*cdist;

double y1 = uv_norm(1)*cdist;

uv_dist(0) = cam_d(0)*x1 + cam_d(2);

uv_dist(1) = cam_d(1)*y1 + cam_d(3);

} else {

// Calculate distorted coordinates for radial

double r = std::sqrt(uv_norm(0)*uv_norm(0)+uv_norm(1)*uv_norm(1));

double r_2 = r*r;

double r_4 = r_2*r_2;

double x1 = uv_norm(0)*(1+cam_d(4)*r_2+cam_d(5)*r_4)+2*cam_d(6)*uv_norm(0)*uv_norm(1)+cam_d(7)*(r_2+2*uv_norm(0)*uv_norm(0));

double y1 = uv_norm(1)*(1+cam_d(4)*r_2+cam_d(5)*r_4)+cam_d(6)*(r_2+2*uv_norm(1)*uv_norm(1))+2*cam_d(7)*uv_norm(0)*uv_norm(1);

uv_dist(0) = cam_d(0)*x1 + cam_d(2);

uv_dist(1) = cam_d(1)*y1 + cam_d(3);

}

 우리는 else 부분만 보면 되며, 방사왜곡된 features의 uv coordinate를 구한다.

 

// Our residual

Eigen::Matrix<double,2,1> uv_m;

uv_m << (double)feature.uvs[pair.first].at(m)(0), (double)feature.uvs[pair.first].at(m)(1);

res.block(2*c,0,2,1) = uv_m - uv_dist;

 normalize된 uv coordinate에서 방사왜곡된 uv coordinate를 뺌으로써 residual을 구하게 된다.

 

// If we are doing first estimate Jacobians, then overwrite with the first estimates

if(state->_options.do_fej) {

R_GtoIi = clone_Ii->Rot_fej();

p_IiinG = clone_Ii->pos_fej();

//R_ItoC = calibration->Rot_fej();

//p_IinC = calibration->pos_fej();

p_FinIi = R_GtoIi*(p_FinG_fej-p_IiinG);

p_FinCi = R_ItoC*p_FinIi+p_IinC;

//uv_norm << p_FinCi(0)/p_FinCi(2),p_FinCi(1)/p_FinCi(2);

//cam_d = state->get_intrinsics_CAM(pair.first)->fej();

}

 fej를 사용하는 경우 값을 가져온다.

 

// Compute Jacobians in respect to normalized image coordinates and possibly the camera intrinsics

Eigen::Matrix<double,2,2> dz_dzn = Eigen::Matrix<double,2,2>::Zero();

Eigen::Matrix<double,2,8> dz_dzeta = Eigen::Matrix<double,2,8>::Zero();

UpdaterHelper::get_feature_jacobian_intrinsics(state, uv_norm, state->_cam_intrinsics_model.at(pair.first), cam_d, dz_dzn, dz_dzeta);

 jacobian을 계산한다.

 

// Normalized coordinates in respect to projection function

Eigen::Matrix<double,2,3> dzn_dpfc = Eigen::Matrix<double,2,3>::Zero();

dzn_dpfc << 1/p_FinCi(2),0,-p_FinCi(0)/(p_FinCi(2)*p_FinCi(2)),

0, 1/p_FinCi(2),-p_FinCi(1)/(p_FinCi(2)*p_FinCi(2));

 

// Derivative of p_FinCi in respect to p_FinIi

Eigen::Matrix<double,3,3> dpfc_dpfg = R_ItoC*R_GtoIi;

 camera frame에서 features를 구한다.

 

// Derivative of p_FinCi in respect to camera clone state

Eigen::Matrix<double,3,6> dpfc_dclone = Eigen::Matrix<double,3,6>::Zero();

dpfc_dclone.block(0,0,3,3).noalias() = R_ItoC*skew_x(p_FinIi);

dpfc_dclone.block(0,3,3,3) = -dpfc_dpfg;

 camera feame에 대한 features를 구하는데, camera clone의 state에 대해 구한다...

 

// Precompute some matrices

Eigen::Matrix<double,2,3> dz_dpfc = dz_dzn*dzn_dpfc;

Eigen::Matrix<double,2,3> dz_dpfg = dz_dpfc*dpfc_dpfg;

 미리 계산

 

// CHAINRULE: get the total feature Jacobian

H_f.block(2*c,0,2,H_f.cols()).noalias() = dz_dpfg*dpfg_dlambda;

 

// CHAINRULE: get state clone Jacobian

H_x.block(2*c,map_hx[clone_Ii],2,clone_Ii->size()).noalias() = dz_dpfc*dpfc_dclone;

 

// CHAINRULE: loop through all extra states and add their

// NOTE: we add the Jacobian here as we might be in the anchoring pose for this measurement

for(size_t i=0; i<dpfg_dx_order.size(); i++) {

H_x.block(2*c,map_hx[dpfg_dx_order.at(i)],2,dpfg_dx_order.at(i)->size()).noalias() += dz_dpfg*dpfg_dx.at(i);

}