Information/Paper

[Paper] A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation

페트론 2020. 11. 27. 18:15

A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation

 

Anastasios I. Mourikis and Stergios I. Roumeliotis

 

Abstract

  • 본 논문에서는 real-time vision-aided inertial navigation을 위한 Extended Kalman Filter (EKF) 기반의 알고리즘을 소개한다. 
  • 이 작업의 주된 내용은 여러 카메라 포즈에서 정적인 특징들을 관측할 때 발생하는 기하학적 제한들을 표현하여 EKF의 측정 모델(measurement model)을 유도하는 것이다.
  • 이 측정 모델은 EKF의 state vector에서 3차원 특징 좌표를 포함할 필요가 없으며, 선형 에러(linearization errors)까지 최적화 시킨다.
  • 본 논문에서 제시한 vision-aided inertial navigation 알고리즘은 오직 선형적으로 특징점 개수만큼만 연산적인 복잡도를 갖으며, large-scale real-world 환경에 대해 높은 정밀도로 포즈를 추정하는 것이 가능하다.
  • 알고리즘의 성능은 urban area에서 camera/IMU 시스템의 위치인식을 한 실험의 결과에 소개되어 있다.

1. Introduction

 

2. Related Work

 

3. Estimator Description

  • 제안된 EKF-based estimator의 목표는 {G}로 표현되는 global frame에 대한 IMU 프레임 3D pose {I}를 tracking 하는 것이다.
  •  알고리즘에 대한 개요는 Algorithm 1에서 확인할 수 있다.
Algorithm 1 Multi-State Constraint Filter
Propagation: 매번 얻어지는 IMU measurement에 대해  filter state와 covariance를 propagate 한다. (cf. Section 3-B)

Image registration: 매번 새로운 이미지가 얻어지면,
    - 현재 추정된 카메라 포즈의 copy와 함께 state와 covariance matrix를 증가(augment)시킨다. (cf. Section 3-C).
    - 이미지 처리 모듈의 작업을 시작한다.

Update: 얻어진 이미지에 대해 특징이 검출되었다면, EKF update를 수행한다. (df. Sections 3-D)

 

  • 그러므로, 모든 시간의 EKF state vector instant는 다음과 같이 구성된다.
    1. 서서히 전개되는 IMU state를 의미하는 X_IMU
    2. N_max 개의 과거 camera poses. 

A. Structure of the EKF state vector

  • 서서히 전개되는 IMU state인 X_IMU는 식 (1)과 같이 vector로 표현된다.

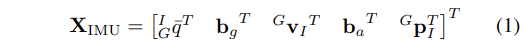
  • 이 때, q는 frame {G}로부터 frame {I}까지의 회전을 표현하는 unit quaternion이며, p와 v는 frame {G}에 대한 IMU의 위치, 속도이다. 마지막으로 b_g와 b_a는 각각 gyroscope와 accelerometer measurements에 대한 biases를 의미하는 3x1 vectors이다. 
  • IMU biases는 각각 white Gaussian noise vectors n_wg, n_wa인 random walk processes로 모델링 된다.
  • IMU error-state는 식 (1)을 따라서 다음과 같은 식 (2)로 정의된다. 

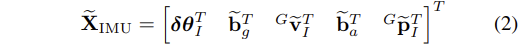
  • 위치, 속도, 바이어스에 대해선 standard additive error definition이 사용된다. 예를 들면 상태 x에 대해 추정된 상태 x_^의 error인 x_~는 다음과 같다. 

 

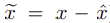
  • 하지만 quaternion에 대해서는 다른 방식의 error definition이 사용된다.
  • q_^-가 q_-에 대해 추정된 값이므로, 회전 error인 error quaternion δq_- 는 다음과 같이 정의된다.

 

  • 여기서 X에 원이 둘러싸인 표시는 quaternion multiplication이 된다.
  • error quaternion은 다음과 같다.

 

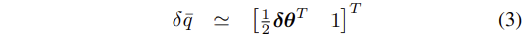
  • 직관적으로 δq_-는 실제 회전과 추정된 회전 사이에 존재하는 작은 크기의 회전이 된다.
  • 자세정보는 3자유도이므로, δθ를 사용하는 것은 자세 error에 대한 최소한의 표현이 된다.
  • N camera poses들은 time-step k에서의 EKF state vector에 포함되어 있다고 가정하면, vector는 다음과 같은 형태가 된다.

 

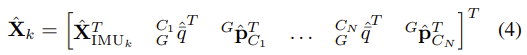
  • i = 1 ... N 일때 q와  p들은 각각 추정된 카메라의 자세와 위치가 된다.
  • 따라서 EKF error-state vector는 다음과 같다.  

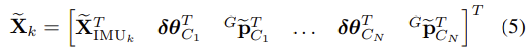
B. Propagation

  • filter propagation equations은 아래와 같이 continuous-time IMU system model의 이산화(discretization)로 유도된다. 

1. Continuous-time system modeling

  • IMU state의 시간변화는 다음과 같이 나타난다[20].

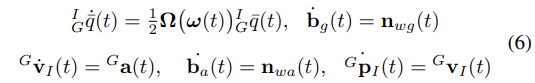
  • 여기서 a는 global frame에서의 body acceleration이 되고, w=[wx, wy, wz]T는 IMU frame에서의 회전 속도가 된다.

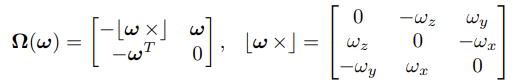
  • gyroscope와 accelerometer measurements인 w_m과 a_m은 [20]을 통해 다음과 같이 주어진다.

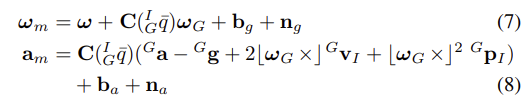
  • C는 회전 행렬을 나타내며, n_g와 n_a는 zero-mean, white Gaussian noise processes modeling을 나타낸다.
  • IMU measurements에 지구의 회전을 의미하는 w_G를 포함시키는 것이 중요하다.
  • 게다가 accelerometer measurements의 경우 local frame에서 g_G로 표현되는 중력 가속도를 포함시키게 된다.
  • 식 (6)의 state propagation equations을 적용함으써, IMU state를 추정하기 위한 propagating equations을 얻을 수 있다.

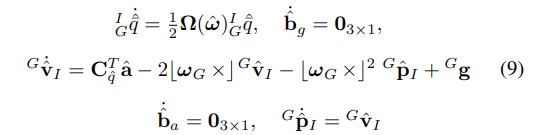
  • 간결성을 위해 다음과 같이 수식들을 표현한다.

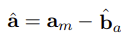
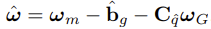
  • IMU error-state 를 위한 linearized continuous-time model은 다음과 같다. 이 때, n_IMU = [n_g n_wg n_a n_wa] 가 system noise가 된다. 

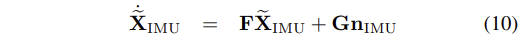
  • n_IMU의 covariance matrix인 Q_IMU는 off-line의 sensor calibration을 통해 얻어지는 IMU noise 특성에 의존한다.
  • 최종적으로, Eq.(10)의 행렬 F와 G는 다음과 같이 구해진다. 이 때, I_3는 3x3 identity matrix이다.

 

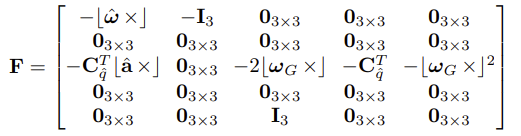
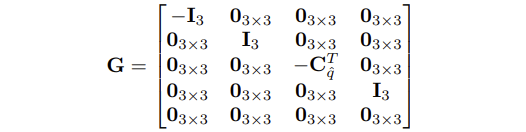
2. Discrete-time implementation

  • IMU는 period T 간격으로 신호 w_m과 a_m을 샘플링하게 되며, 이러한 측정 값들은 EKF에서 state propagation에 사용된다.
  • 매번 새로운 IMU measurement가 받아지면, IMU state estimate가 식 (9)를 이용한 5th order Runge-Kutta numerical integration을 사용하여 propagate된다.
  • 게다가 EKF covariance matrix도 propagate 된다.
  • 이러한 목적을 위해, 다음의 분할된 covariance를 소개한다.

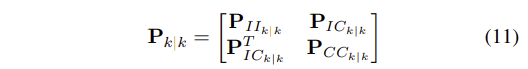
  • (0,0)은 evolving IMU state의 15x15 크기 covariance matrix
  • (1,1)은 camera pose estimates의 6N x 6N 사이즈 covariance matrix
  • (0,1) & (1,0)은 IMU state와 camera pose estimates 간의 error 관계이다.
  • 다음과 같은 방법으로 propagated state의 covariance matrix가 주어진다.

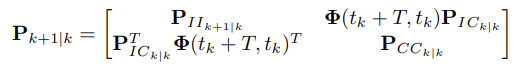
  • 이 때, (0,0)은 Lyapunov equation의 numerical integration에 의해 다음과 같이 계산된다.

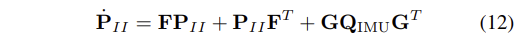
  • Numerical integration는 (0,0)인 초기조건을 사용하여 time interval (t_k, t_k+T)동안 이루어진다.
  • state transition matrix Φ는 비슷하게 차동 방정식(differential equation)의 수치 적분(numerical integration)을 이용하게 된다. 이 때 초기화 조건은 Φ(t_k,t_k)=I_15가 된다.

C. State Augmentation

 

  • 새로운 이미지를 받기 전, 식 (14)와 같이 IMU pose estimate 로부터 camera pose estimate를 계산하게 된다.

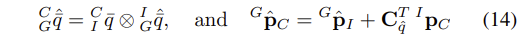
  • 이 때, CI_q_- 는 IMU와 camera frame 사이의 회전을 나타내는 quaternion이며, I_p_C는 IMU frame {I}에 대한 camera frame의 origin의 위치가 된다.  
  • 이러한 camera pose estimate는 state vector에 추가되고, EKF의 공분산 행렬(covariance matrix)이 그에 따라 증가된다.

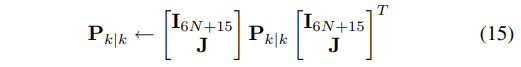
  • 이 때, Jacobian J는 식(14)로부터 유도된다.

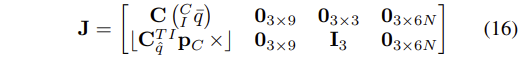
D. Measurement Model

  • 이제 measurement model이 어떻게 state estimates updating에 사용되는지 소개한다. 이는 본 논문의 주요 내용이 된다.
  • EKF가 state estimation에 사용되기 때문에, measurement model을 만들기 위해서는 residual "r"을 설정하는 것만으로도 충분하다. "r"은 선형적으로 state errors "X_~"에 의존하므로 일반형은 다음과 같게 된다.

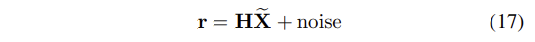
  • 식 (17)에서 H는 measurement Jacobian matrix이며, noise는 EKF framework에 적용하기 위해 반드시 zero-mean, white Gaussian noise이고, state error와 관계가 없어야 한다. 
  • measurement model을 유도하기 위해서, multiple camera poses로부터 정적인 특징(static feature)을 관측하게 되면 모든 poses에 대해 제약 조건(constraints)이 생긴다는 것에 동기부여를 받았다.
  • 이 작업에서, camera observations은 measurements가 관측되는 per camera pose 보다는 per tracked feature로 묶었다. (per camera pose의 경우는 포즈간의 제약을 계산하는 방법이다[7], [13], [14].)
  • 모든 3D point의 관측값(measurements)들과 관측값이 발견된 모든 camera poses들은 constraint equation (cf. Eq. (24))를 정의하는데에 사용된다.
  • 이는 filter state vector에 feature position을 포함하지 않고도 얻어진다.

    (글쓴이 : filter state vector가 커질수록 연산량은 증가하기 때문에, 3d feature position이 아닌 이미지의 특징 좌표를 state vector에 포함시켜 사용하는 것은 연산적으로 매우 이득이다.)
  • 해당 measurement model은 모든 M_j camera poses들의 set에서 발견된 하나의 특징(feature) f_j를 고려하게 된다. 이 때, camera poses는 아래와 같이 구성된다.

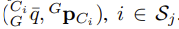
  • 특징의 각 M_j observations은 식 (18)과 같은 모델로 설명된다.

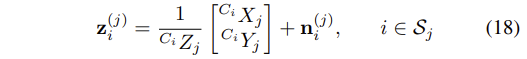
  • 이 때, n_i_(j)는  covariance matrix R_i_(j)가 있는 2x1 image noise vector이다.
  • camera frame Ci_p_fj에 표현된 feature position은 다음과 같다. 

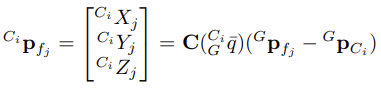
  • 이 때, G_p_fj는 global frame 에서의 3D feature position이다.
  • G_p_fj를 알 수 없기 때문에, 알고리즘의 첫번째 단계에서 least-squares minimization을 사용해 feature position의 estimate, G_p_^fj를 얻어내게 된다. 
  • 이는 measurements z_i_(j)와 해당 time instants의 camera poses의 filter estimate를 사용하여 얻어진다. (cf.Appendix)
  • 일단 feature position의 estimate가 얻어지면, measurement residual을 계산하게 된다.

  • 이 때, z_^_i_(j)는 다음과 같다.

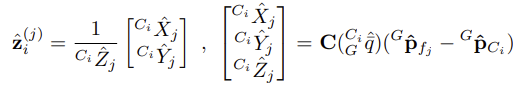
  • camera pose와 feature position을 위한 estimates에 대한 선형화를 위해, Eq.(20)의 residual은 다음과 같이 근사될 수 있다.

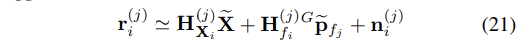
  • 위 수식에서 H_Xi(j)와 H_fi(j)는 각각 상태(state)와 feature position에 대한 measurement z_i(j)의 Jacobians이며, G_~p_fj는 f_j의 position estimate의 error이다.
  • 위 수식의 Jacobians에 대한 정확한 값은 [21]에 나와있다.
  • 해당 feature의 모든 관측값(measurements) M_j의 residual을 모으면 다음의 결과를 얻을 수 있다.

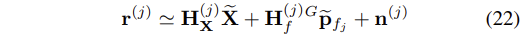
  • 이 때, r_(j), H_X(j), H_f(j), n_(j) 들은 elements r_i(j), H_Xi(j), H_fi(j), n_i(j)를 갖는 block vectores 혹은 matrices이다. 이 때 i는 S_j의 부분집합이다.
  • 서로 다른 이미지들에 존재하는 feature observations들은 독립적이기 때문에, n_(j)의 covariance matrix R_(j)는 다음과 같다.

  • state estimate X가 feature position estimate(cf. Appendix)에 사용되기 때문에, Eq.(22)의 error G_~p_fj는 errors ~X와 관련된다.
  • 그러므로 residual r_(j)는 Eq.(17)의 형태가 아니며, EKF의 measurement updates에 바로 적용될 수 없다.
  • 이러한 문제점을 극복하기 위해, 본 논문에서는  residual r_o(j)를 행렬 H_f(j)의 left nullspace에 사영시킴으로써 residual r_o(j)를 정의하게 된다. 
  • 특히, 행렬 A를 행렬 H_f의 left nullspace의 기저를 형성하는 columns을 갖는 단위 행렬로 나타낸다면 우리는 아래와 같은 수식을 얻을 수 있다.

  • 2M_j X 3 행렬인 H_j(j)는 full column rank이므로, H_j(j)의 left nullspace는 2M_j - 3 차원이 된다.
  • 그러므로 r_o(j)는 (2M_j - 3) X 1 vector가 된다.
  • 해당 residual은 feature coordinates의 errors에서 독립적이고, 그렇기 때문에 이를 기반으로 EKF updates를 수행하는 것이 가능하다.
  • Eq.(24)는 feature f_j가 관측된 모든 camera poses 사이의 선형적 제한(linearized constraint)을 정의한다.
  • 이는 measurements z_i(j)가 M_ states를 위해 제공하는 모든 가능한 정보를 의미하며, 그러므로 선형화(linearization)에 의해 생기는 부정확함(inaccuracies)을 제외한 EKF update가 최적화된다.
  •  언급하고 넘어가야할 부분은, residual r_o(j)와 measurement matrix H_o(j)를 계산하기 위해, 단위 행렬(unitary matrix) A가 꼭 명확하게 평가되어야할 필요는 없다는 것이다.
  • 그 대신에, H_f(j)의 nullspace에 대한 vector r과 행렬(matrix) H_X(j)의 사영을 이용하면 O(M_j2) operations[22]를 통해 매우 효율적으로 계산이 가능하다.
  • 추가적으로, 행렬 A가 단위(unitary) 행렬이기 때문에, noise vector n_o(j)의 공분산 행렬(covariance matrix)은 다음과 같아진다. 

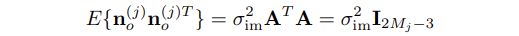
  • Eq. (23)에 정의된 residual은 M_j 이미지의 정적인 특징을 얻어냄으로써 발생하는 기하학적 제한(geometric constraints)를 표현하는 유일한 방법이 아니다.
  • 대체 가능한 접근으로, 예를 들면, 각각 M_j(M_j - 1)/2 pairs of images에 대한 epipolar constraints이 정의된다.
  • 그러나 각각의 measurement가 여러번 사용되므로 방정식이 통계적으로 상관성을 갖으므로 M_j(M_j - 1)/2 equations은 여전히 2M_j - 3의 독립적인 제한하고만 연관성을 갖게 된다.
  • 실험에서 epipolar constraints의 linearization을 사용하는 것이 기존의 방법보다 훨씬 복잡한 과정을 거쳐야하고, 더 낮은 결과를 도출한다는 것을 증명하였다.

E. EKF Updates

  • 앞의 섹션에서 여러 카메라 포즈로 부터 얻어진 중첩되는 정적인 특징(static feature)을 관측함으로써 기하학적 제한(geometric constraints)를 표현하는 측정 모델(measurement model)을 소개하였다.
  • 이제 관측된 여러 특징(features)로부터 얻어진 제한(constaints)을 이용해 EKF를 갱신(update)하는 부분에 대해 자세히 소개한다.
  • EKF 갱신(updates)는 아래의 두가지 이벤트 중 하나가 발생하게되면 이루어진다.
    •  첫번째이벤트
      • 여러 이미지에서 추적된 특징점이 더 이상 검출되지 않게 되면 해당 특징에 대한 모든 측정값(measurements)들은 섹션 3-D의 기법으로 진행된다.
      • 이런 경우는 특징이 카메라의 관측범위(field of view)에서 벗어나게 되면 매우 빈번하게 일어나게 된다.
    • 두번째 이벤트
      • 매번 새로운 이미지가 얻어지면, 현재 추정된 카메라 포즈(camera pose estimate)의 copy는 state vector에 포함되게 된다. (cf. Section 3-C)
      • 만약 최대 개수의 카메라 포즈(N_max)가 얻어지면, 최소 한 개의 오래된 포즈가 제거된다.
      • 상태(states)를 제거하기 전에, 위치인식 정보에 활용하기 위하여 해당 시간에서 일어난 모든 특징 관측(feature observations)을 사용한다.
      • 해당 알고리즘에서, 두번째로 오래된 포즈부터 시작 포즈까지 N_max/3 개의 포즈가 균등한 시간간격으로 선택된다. 
      • 이 포즈들에 공통적으로 존재하는 특징(features)의 제약(constraints)를 사용하는 EKF 갱신(update)이 수행된 후, 해당 포즈들은 버려지게 된다.
      • 본 논문에서는 가장 오래된 state vector의 포즈를 유지하게 되는데, 왜냐하면 포즈와 관련된 기하학적 제약(geometric constraints)는 일반적으로 오래될수록 큰 기준점이 되기 때문이며, 더 가치있는 위치 정보(positioning information)을 얻기 때문이다.
      • 이러한 접근법은 실험에서도 잘 작동하는 것을 보여준다.
  • 이제 갱신 과정(update process)에 대해 자세히 이야기해보자.
  • 위 두 기준에 의해 선택된 주어진 time step에서 L features의 제약(constraints)이 반드시 이루어진다고 하자.
  • 앞의 섹션에서 설명된 과정을 따르면, 우리는 각 특징(features)에 대한 residual vector r_o(j), j=1...L와 이와 관련된 measurement matrix H_o(j), j=1...L을 계산하고 싶다(cf. Eq. (23)). 
  • 모든 residuals을 single vector에 쌓으면 다음과 같은 수식을 얻을 수 있다. 

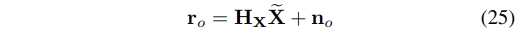
  • 이 때, r_o와 n_o는 각각 block elements r_o(j)와 n_o(j)로 만들어진 vectors가 되고, H_x는 block rows H_x(j), j=1...L로 이루어진 행렬이 된다.
  • 특징 측정(feature measurements)은 통계적으로 독립적이기 때문에, noise vectors n_o(j)는 상관이 없다.
  • 그러므로, noise vector n_o의 공분산 행렬(covariance matrix)은 다음과 같으며, residual r_o의 크기(차원)를 갖는다.

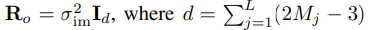
  • 실제에서 발생할 수 있는 하나의 문제는, d가 매우 큰 수가 될 수도 있다는 것이다.
  • 예를들어, 10개의 포즈에서 각각 10개씩의 특징(features)이 발견되면, residual의 크기(차원,dimension)은 170이 된다.
  • EKF 갱신(Update)의 연산량을 줄이기 위해, 본 논문에서는 H_X의 QR decomposition을 이용한다[9].
  • 특별히, 해당 분해(decomposition)을 다음과 같이 표기한다.

  • 이 때, Q_1과 Q_2는 열이 각각 H_x의 range와 nullspace에 대한 밑(bases)을 형성하는 단위 행렬(unitary matrices)이 되며, T_H는 윗삼각행렬(upper triangular matrix)이 된다.
  • 이러한 정의와 함께 Eq.(25) 을 이용하면 다음의 수식이 얻어진다.

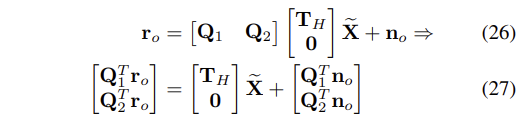
  • 마지막 방정식을 살펴보면 residual r_o를 H_x의 range의 기저벡터에 사영시킴으로써 measurements에서 모든 유용한 정보를 얻을 수 있다는 것을 확실히 알 수 있다.
  • residual Q_2T r_o는 단순 노이즈고, 전부 버려도 된다.
  • 이러한 이유에서 EKF 갱신(update)에서 Eq.(25)의 residual 대신에 본 논문은 다음의 residual을 사용한다.

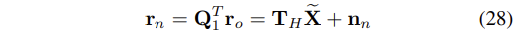
  • 위 수식에서 n_n = Q_1T n_o는 노이즈 벡터이며, n_n의 공분산 행렬(covariance matrix)는 다음과 같다.

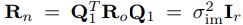
  • 이 때, r은 Q_1의 columns의 개수가 된다.
  • Kalman gain을 계산함으로써 EKF 갱신(update)는 다음과 같이 진행된다.

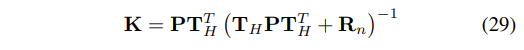
  • state의 수정은 vector에 의해 이루어진다.

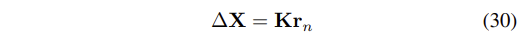
  • 마지막으로, 상태 공분산 행렬(state covariance matrix)는 다음과 같이 update 된다.

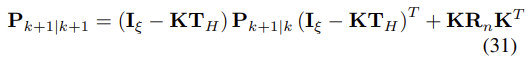
  • 이 때, ξ = 6N+15는 공분산 행렬(covariance matrix)의 크기(차원)이 된다.

 

F. Disscussion

 

4. Experimental Results

 

5. Conclusions

From IEEE (ieeexplore.ieee.org/document/4209642/references#references)

 

1.J. W. Langelaan, "State estimation for autonomous flight in cluttered environments," Ph.D. dissertation, Stanford University, Department of Aeronautics and Astronautics, 2006.

Show Context CrossRef  Google Scholar 

2.D. Strelow, "Motion estimation from image and inertial measurements," Ph.D. dissertation, Carnegie Mellon University, 2004.

Show Context CrossRef  Google Scholar 

3.L. L. Ong, M. Ridley, J. H. Kim, E. Nettleton, and S. Sukkarieh, "Six DoF decentralised SLAM," in Australasian. Conf. on Robotics and Automation, Brisbane, Australia, December 2003, pp. 10-16.

Show Context Google Scholar 

4.E. Eade and T. Drummond, "Scalable monocular SLAM," in IEEE Computer Society Conference on Computer Vision and Pattern. Recognition, June 17-26 2006, pp. 469 - 476.

Show Context View Article Full Text: PDF (663KB) Google Scholar 

5.A. Chiuso, P. Favaro, H. Jin, and S. Soatto, "Structure from motion causally integrated over time," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 24, no. 4, pp. 523-535, April 2002.

Show Context View Article Full Text: PDF (376KB) Google Scholar 

6.A. J. Davison and D. W. Murray, "Simultaneous localisation and mapbuilding using active vision," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 24, no. 7, pp. 865 - 880, July 2002.

Show Context View Article Full Text: PDF (4187KB) Google Scholar 

7.S. Roumeliotis, A. Johnson, and J. Montgomery, "Augmenting inertial navigation with, image-based motion estimation," in IEEE International Conference on Robotics and Automation, Washington D.C., 2002, pp. 4326-33.

Show Context View Article Full Text: PDF (913KB) Google Scholar 

8.D. D. Diel, "Stochastic constraints for vision-aided inertial navigation," Master's thesis, MIT, January 2005.

Show Context View Article Full Text: PDF (679KB) Google Scholar 

9.D. S. Bayard and P. B.Brugarolas, "An estimation algorithm for visionbased exploration of small bodies in space," in American, Control Conference, June 8-10 2005, pp. 4589 - 4595.

Show Context View Article Full Text: PDF (690KB) Google Scholar 

10.S. Soatto, R. Frezza, and P. Perona, "Motion estimation via dynamic vision," IEEE Transactions on Automatic Control, vol. 41, no. 3, pp. 393-413, March 1996.

Show Context View Article Full Text: PDF (2325KB) Google Scholar 

11.S. Soatto and P. Perona, "Recursive 3-d visual motion estimation using subspace constraints," IEEE Transactions on Automatic Control, vol. 22, no. 3, pp. 235-259, 1997.

Show Context Google Scholar 

12.R. J. Prazenica, A. Watkins, and A. J. Kurdila, "Vision-based kalman filtering for aircraft state estimation and structure from motion," in Proceedings of the AIAA Guidance, Navigation, and Control Conference, no. AIAA 2005-6003, San Fransisco, CA, Aug. 15-18 2005.

Show Context

13.R. Garcia, J. Puig, P. Ridao, and X. Cufi, "Augmented state Kalman filtering for AUV navigation," in IEEE International Conference on Robotics and Automation, Washington D.C., 2002, pp. 4010-4015.

Show Context View Article Full Text: PDF (623KB) Google Scholar 

14.R. Eustice, H. Singh, J. Leonard, M. Walter, and R. Ballard, "Visually navigating the RMS Titanic with SLAM information filters," in Proceedings of Robotics: Science and Systems, Cambridge, MA, June 2005.

Show Context Google Scholar 

15.A. I. Mourikis and S. I. Roumeliotis, "On the treatment of relative-pose measurements for mobile robot localization," in Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, May 15-19 2006, pp. 2277 - 2284.

Show Context View Article Full Text: PDF (556KB) Google Scholar 

16.D. Nister, O. Naroditsky, and J. Bergen, "Visual odometry for ground vehicle applications," Journal of Field Robotics, vol. 23, no. 1, pp. 3-20, January 2006.

Show Context CrossRef  Google Scholar 

17.P. McLauchlan, "The variable state dimension filter," Centre for Vision, Speech and Signal Processing, University of Surrey, UK, Tech. Rep., 1999.

Show Context Google Scholar 

18.M. C. Deans, "Maximally informative statistics for localization and mapping," in IEEE International Conference on Robotics and Automation, Washington D.C., May 2002, pp. 1824-1829.

Show Context View Article Full Text: PDF (545KB) Google Scholar 

19.W. G. Breckenridge, "Quaternions proposed standard conventions," JPL, Tech. Rep. INTEROFFICE MEMORANDUM IQM 343-79-1199, 1999.

Show Context Google Scholar 

20.A. B. Chatfield, Fundamentals of High Accuracy Inertial Navigation. Reston, VA: AIAA, 1997.

Show Context CrossRef  Google Scholar 

21.A. I. Mourikis and S. I. Roumeliotis, "A multi-state constraint kalman filter for vision-aided inertial navigation," Dept. of Computer Science and Engineering, University of Minnesota, Tech. Rep., 2006, www.cs.umn.edu/~mourikis/tech-reports/TR-MSCKF.pdf.

Show Context

22.G. Golub and C. van Loan, Matrix computations. The Johns Hopkins University Press, London, 1996.

Show Context Google Scholar 

23.J. Oliensis, "A new structure-from-motion ambiguity," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 22, no. 7, pp. 685-700, July 2000.

Show Context View Article Full Text: PDF (793KB) Google Scholar 

24.A. Huster, "Relative position sensing by fusing monocular vision and inertial rate sensors," Ph.D. dissertation, Department of Electrical Engineering, Stanford University, 2003.

Show Context Google Scholar 

25.A. D. J. Montiel, J. Civera, "Unified inverse depth parametrization for monocular slam," in Proceedings of Robotics: Science and Systems, Philadelphia, PA, June 2006.

Show Context Google Scholar 

26.http://www.cs.umn.edu/~mourikis/icra07video.htm.

Show Context

27.D. G. Lowe, "Distinctive image features from scale-ivnariant keypoints," Inter-national Journal of Computer Vision, vol. 60, no. 2, pp. 91-100, 2004.

Show Context CrossRef  Google Scholar 

28.B. Triggs, P. McLauchlan, R. Hartley, and Fitzgibbon, "Bundle adjustment - a modern synthesis," in Vision. Algorithms: Theory and Practice. Springer Verlag, 2000, pp. 298-375.

CrossRef  Google Scholar 

반응형